What is Dynamic Programming?

For me, DP problem is the most challenging problem when I faced it during the interview process. To understand it I summarize basic concepts and patterns.

Simply It can be defined,

Dynamic Programming = Complex problems -> smaller subproblem

Dynamic Programming vs Divide and Conquer

Key difference

Dynamic Programming – has overlapping sub problems

Dynamic Programming Paradigm

Optimal Substructure

In computer science, a problem is said to have optimal substructure if an optimal solution can be constructed from optimal solutions of its subproblems. This property is used to determine the usefulness of greedy algorithms for a problem.
WIKIPEDIA

It can solve these kinds of problems

Greedy approach

Bellman Equation (Combinatorial optimization)

Bellman showed that a dynamic optimization problem in discrete time can be stated in a recursive, step-by-step form known as backward induction by writing down the relationship between the value function in one period and the value function in the next period. The relationship between these two value functions is called the “Bellman equation”.
WIKIPEDIA

It can solve these kinds of problems

0-1 Knapsack problem

What is overlapping subproblems?

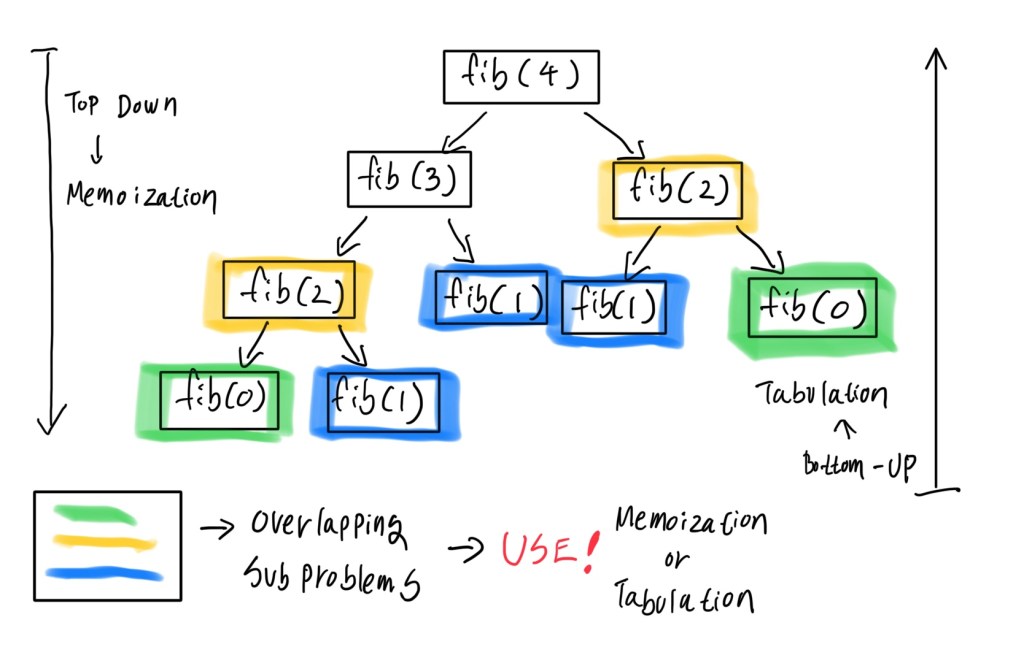
Let’s see fibonacci problem.

fib(n) = fib(n-1) + fib(n-2)

//Base case
fib(0) = 0
fib(1) = 1

To get the fib(n), we need to call fib(n-1) and fib(n-2) and then sum it.

Colored boxes are overlapped sub problems. Because It was called multiple times.

How to avoid multiple calling overlapped subproblems?

Answer: Save the result and use it without calling a function or recalculating it.

Top-Down Approach: Memoization (Recursion)

Memoization you can implement using Array or Dictionary. In Swift, You have to handle it carefully like out of bounds.

class Fibonacci {
  func fib(_ n: Int) -> Int {
    var memoization = Array(repeating: 0, count: n + 1)
    func recursiveFib(
      _ n: Int, 
      memoization: inout [Int]
    ) -> Int {
      if memoization[n] != 0 {
        return memoization[n]
      }
      if n < 2 {
        memoization[n] = n
        return n
      }
      let sum = recursiveFib(n-1, memoization: &memoization) + recursiveFib(n-2, memoization: &memoization)
      memoization[n] = sum
      return sum
    }
    return recursiveFib(n, memoization: &memoization)
  }
}

let fibonacci = Fibonacci()
let result = fibonacci.fib(7) //Result is 13

I prefer to use dictionary for memoization. It’s more safe and easy to save the result of subproblems.

class Fibonacci {
  var memoization = [Int: Int]()
  func fib(_ n: Int) -> Int {
    if let value = memoization[n] {
        return value
    }
    if n < 2 {
      memoization[n] = n
      return n
    }
    let sum = fib(n-1) + fib(n-2)
    memoization[n] = sum
    return sum
  }
}

let fibonacci = Fibonacci()
let result = fibonacci.fib(7) //Result is 13

Bottom-Up Approach: Tabulation (avoid recursion)

This approach solve the bottom subproblems first and save the results. You don’t need to use recursion.

class Fibonacci {
  func fib(_ n: Int) -> Int {
    var dp = Array(repeating: 0, count: n + 1)
    //base
    dp[0] = 0
    dp[1] = 1

    for i in 2...n {
      dp[i] = dp[i-1] + dp[i-2]
    }
    return dp[n]
  }
}

let fibonacci = Fibonacci()
let result = fibonacci.fib(7) //Result is 13

[Working in Progress] Dynamic Programming Problem Patterns

Step 1. Understand problem

Step 2. Check Is this problem can be solved by splitting into Sub Problems

Step 3. Is Sub Problems are overlapped?

Step 4. If Yes, It’s DP problem.

Step 5. [Hardest Part] Define a logic when to take an item and do not take an item to reach the solution. -> Don’t memorize the solutions, all the problems we need to define a proper logic by understanding problem.

Step 6. Give a solution (including all taken items)

Knapsack Problem

Divisible Knapsack Problem

Greedy approach can be used

0-1 Knapsack Problem (consider should I take a item or not)

0: Not take an item
1: Take an item

Rod Cutting Problem

References

https://www.udemy.com/share/101AYS3@4sd_kGNnngOfRfF3meBvqpARWBcWTlGxzqIQuKnKpxCDk-bb017OhSQJeotE-YGg/

Shawn