Useful Foundation APIs
- swap the value in an array by passing the index
Bubble Sort
func bubbleSort(input: inout [Int]) {
for i in 0..<input.count {
for j in 1..<input.count {
if input[j] < input[j - 1] {
input.swapAt(j, j-1)
}
}
}
}
var input = [4, 5, 2, 1, 6, 8, 9, 12, 13]
bubbleSort(input: &input)


Every steps compares 2 values and swapped it
Red = Sorted Item
Time complexity is O(n^2)
Space complexity is O(1)
Insertion Sort
Apple Foundation uses TimSort (InsertionSort + MergeSort)


Insertion Sort is another O(N^2) quadratic running time algorithm
On large datasets it is very inefficient – but on arrays with 10-20 items it is quite good. (Apple uses TimSort, It items is less than 64 then use Insertion Sort. -> https://github.com/apple/swift/blob/387580c995fc9844d4f268723bd55e22440b1a3d/stdlib/public/core/Sort.swift#L462)
A huge advantage is that it is easy to implement
It is more efficient than other quadratic running time sorting procedures such as bubble sort or selection sort
It is an adaptive algorithm – It speeds up when array is already substantially sorted
It is stable so preserves the order of the items with equal keys
Insertion sort is an in-place algorithm – does not need any additional memory
It is an online algorithm – It can sort an array as it receives the items for example downloading data from web
Hybrid algorithms uses insertion sort if the subarray is small enough: Insertion sort is faster for small subarrays than quicksort
Variant of insertion sort is shell sort
Sometimes selection sort is better: they are very similar algorithms
Insertion sort requires more writes because the inner loop can require shifting large sections of the sorted portion of the array
In general insertion sort will write to the array O(N^2) times while selection sort will write only O(N) times
For this reason selection sort may be preferable in cases where writing to memory is significantly more expensive than reading (such as with flash memory)



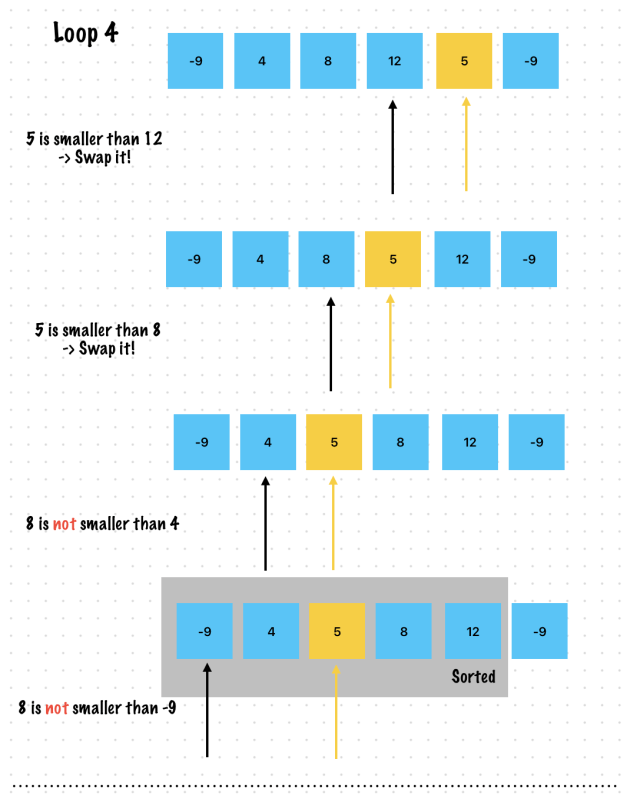


func insertSort(_ input: inout [Int]) {
var i = 1
for i in 1..<input.count {
var j = i
while j-1 >= 0, input[j] < input[j-1] {
input.swapAt(j, j-1)
j-=1
}
}
}
var input = [-9, 4, -9, 5, 8, 12]
insertSort(&input)
print(input)
var input2 = [-9, 4, -9, 5, 8, 12, -249, 241, 4, 2, 12, 24140, 539, 3, 0, -2314]
insertSort(&input2)
print(input2)

Merge Sort
Divide and Conquer
Break down into small subproblem, Use recursion.
It needs two functions
- split – divide into two array
- merge – merging two array into the sorted array
func mergeSort(input: inout [Int]) {
//Base case
if input.count == 1 {
return
}
let midIndex = input.count / 2
var left = Array(repeating: 0, count: midIndex)
var right = Array(repeating: 0, count: input.count - midIndex)
//Split into 2 sub array (create sub problems)
split(input: &input, left: &left, right: &right)
//Recursive - Divide and Conquer
mergeSort(input: &left)
mergeSort(input: &right)
//Merge all together
merge(input: &input, left: &left, right: &right)
}
func split(input: inout [Int], left: inout [Int], right: inout [Int]) {
let leftCount = left.count
for (index, item) in input.enumerated() {
if index < leftCount {
left[index] = item
}
else {
right[index - leftCount] = item
}
}
}
func merge(input: inout [Int], left: inout [Int], right: inout [Int]) {
var mergeIndex = 0
var leftIndex = 0
var rightIndex = 0
while (leftIndex < left.count && rightIndex < right.count) {
if left[leftIndex] < right[rightIndex] {
input[mergeIndex] = left[leftIndex]
leftIndex += 1
}
else if rightIndex < right.count {
input[mergeIndex] = right[rightIndex]
rightIndex += 1
}
mergeIndex += 1
}
if leftIndex < left.count {
while mergeIndex < input.count {
input[mergeIndex] = left[leftIndex]
mergeIndex += 1
leftIndex += 1
}
}
if rightIndex < right.count {
while mergeIndex < input.count {
input[mergeIndex] = right[rightIndex]
mergeIndex += 1
rightIndex += 1
}
}
}

Split Function
Calculate midIndex
Split them into two subarray



Time complexity: O(nlogn)
Space complexity: O(n)
- Because It needs a copy values when merging two array into the one sorted array
Quick Sort
func partition(_ input: inout [Int], low: Int, high: Int) -> Int {
let pivot = input[low]
var l = low
var h = high
while l < h {
while (input[l] <= pivot && l < h) {
l += 1
}
while (input[h] > pivot) {
h -= 1
}
if l < h {
input.swapAt(l, h)
}
}
//Put pivot to the right position
input.swapAt(low, h)
return h
}
func quickSort(_ input: inout [Int], low: Int, high: Int) {
//base
if low >= high {
return
}
//pivot
let pivot = partition(&input, low: low, high: high)
//left
quickSort(&input, low: low, high: pivot - 1)
//right
quickSort(&input, low: pivot + 1, high: high)
}
var input = [2, 3, 1, 4, 9]
quickSort(&input, low: 0, high: input.count - 1)
print(input)
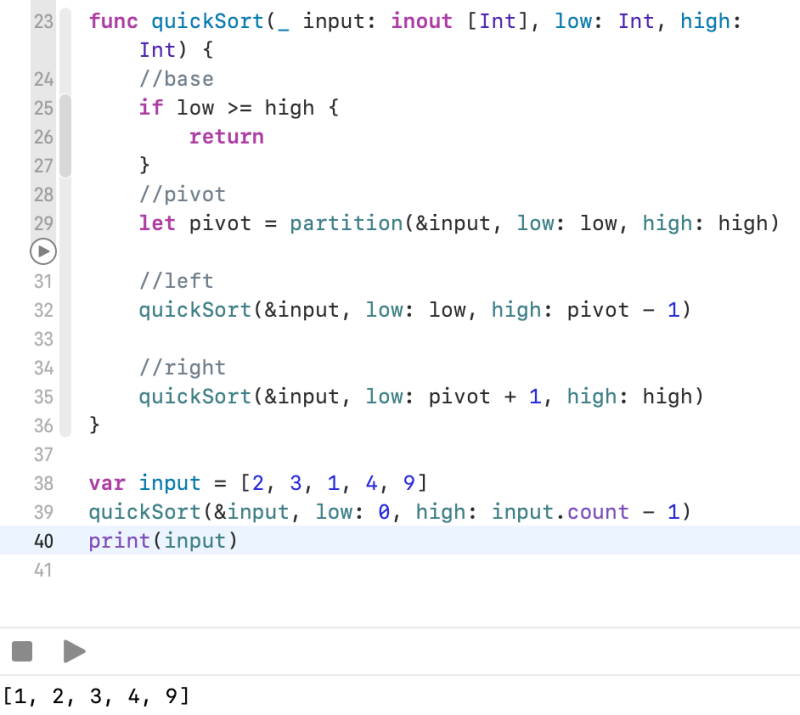

Quick Sort is also Divide and Conquer.
Time Complexity
- Average Time Complexity is O(nlogn)
Space Complexity
- O(logn) -> Extra space for the call stack in the recursive call
- O(n) -> worst case
Binary Search
Search a sorted list!
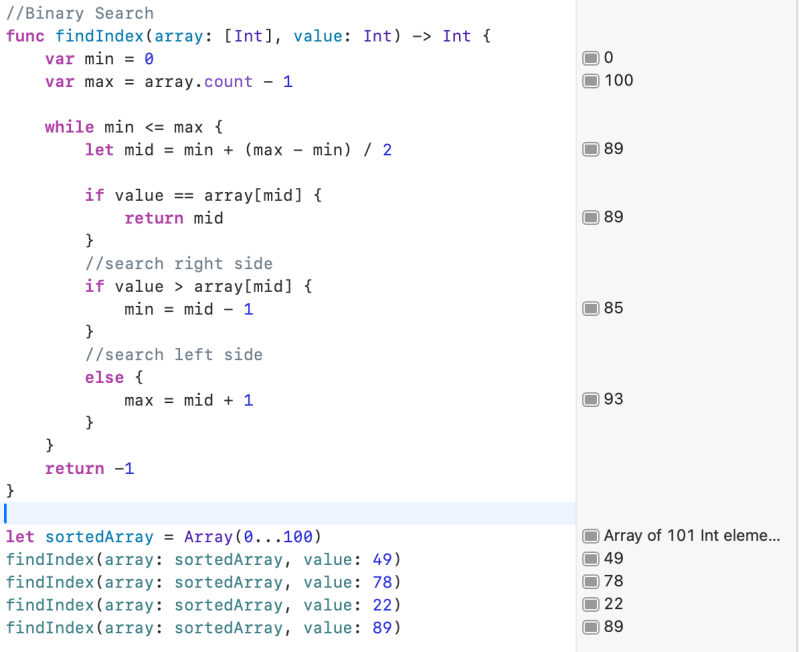
//Binary Search
func findIndex(array: [Int], value: Int) -> Int {
var min = 0
var max = array.count - 1
while min <= max {
let mid = min + (max - min) / 2
if value == array[mid] {
return mid
}
//search right side
if value > array[mid] {
min = mid - 1
}
//search left side
else {
max = mid + 1
}
}
return -1
}
let sortedArray = Array(0...100)
findIndex(array: sortedArray, value: 49)
findIndex(array: sortedArray, value: 78)
findIndex(array: sortedArray, value: 22)
findIndex(array: sortedArray, value: 89)

Leave a comment