✍️ Note
Some codes are sourced from Loony Corn’s Udemy Course (https://www.udemy.com/user/janani-ravi-2/). This post is for personal notes where I summarize the original contents to grasp the key concepts

Tree Data Structure
class Node {
var left: Node?
var right: Node?
var value: Int
init(value: Int) {
self.value = value
}
}
//Create a Tree
let root = Node(value: 5)
root.left = Node(value: 3)
root.right = Node(value: 7)
root.right?.left = Node(value: 6)
root.right?.right = Node(value: 9)
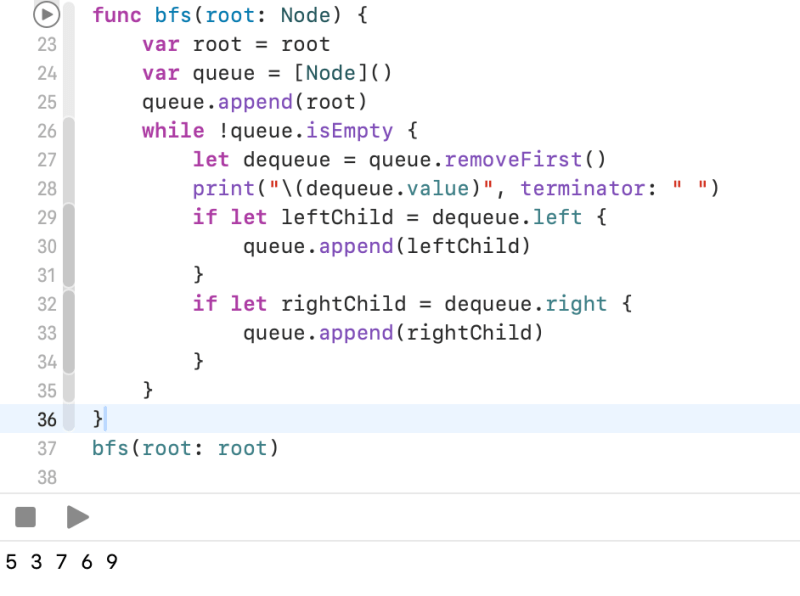
BFS: Breadth First Search
func bfs(root: Node) {
var root = root
var queue = [Node]()
queue.append(root)
while !queue.isEmpty {
let dequeue = queue.removeFirst()
print("\(dequeue.value)", terminator: " ")
if let leftChild = dequeue.left {
queue.append(leftChild)
}
if let rightChild = dequeue.right {
queue.append(rightChild)
}
}
}
bfs(root: root)
DFS: Depth First Search
Use Recursion!
- Define base case -> when the root is null
- Recursion technique -> Processing can be performed
- Before -> Pre-Order
- In-Between or -> In-Order
- After -> Post-Order
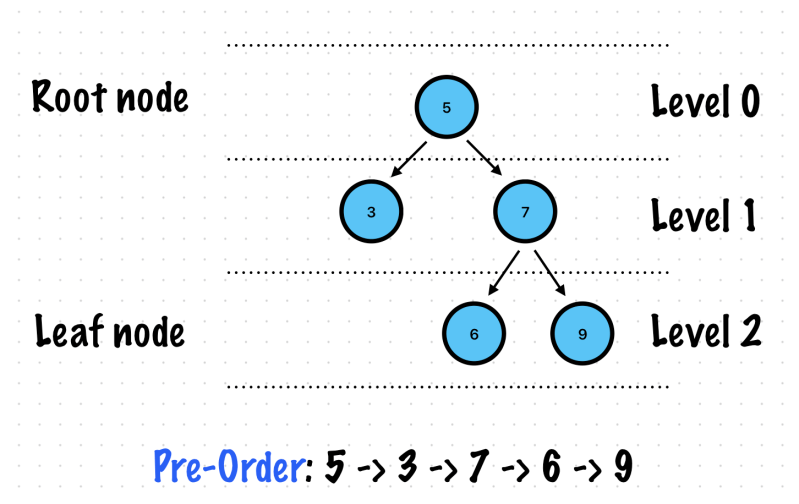
Pre-Order
Each node is processed first (PRE) before It’s right and left subtrees
In-Order


Post-Order
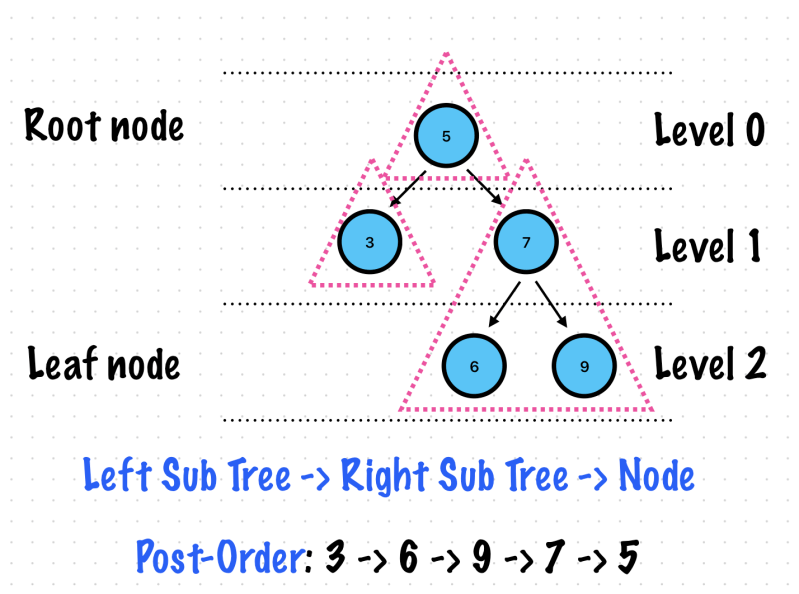
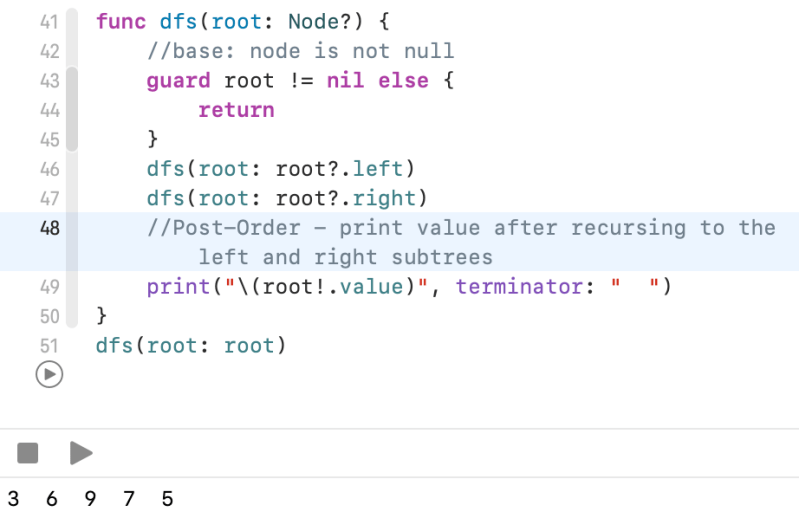
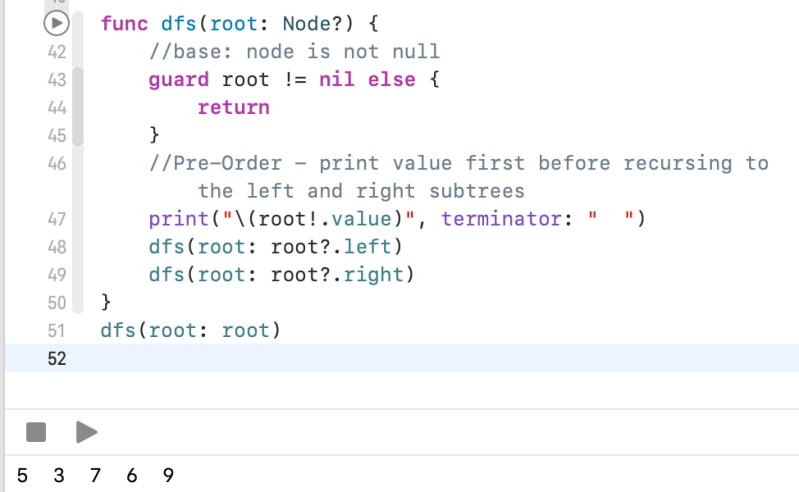
func dfs(root: Node?) {
//base: node is not null
guard root != nil else {
return
}
dfs(root: root?.left)
dfs(root: root?.right)
//Post-Order - print value after recursing to the left and right subtrees
print("\(root!.value)", terminator: " ")
}
dfs(root: root)
//Prints
3 6 9 7 5
Binary Search Tree
It is called an Ordered Binary Tree.
- Each node in the left sub-tree of that node has a value less than or equal to the value of the node
- Each node in the right sub-tree of that node has a value greater than the value of the node
Key Feature
- Typically used for Fast Insertion and Fast Lookup
- Fast Insertion
- In a tree when a new node is added there is exactly one place that it can be
- The structure of a tree depends on the order in which the nodes are added
- Fast Lookup
- While searching for a node in the tree there is only one place where that node can be found
- You can simply follow the right or left sub-trees based on the value you want to find
Insertion
🙏 Below Images are wrong, Level 4 -> Level 3.
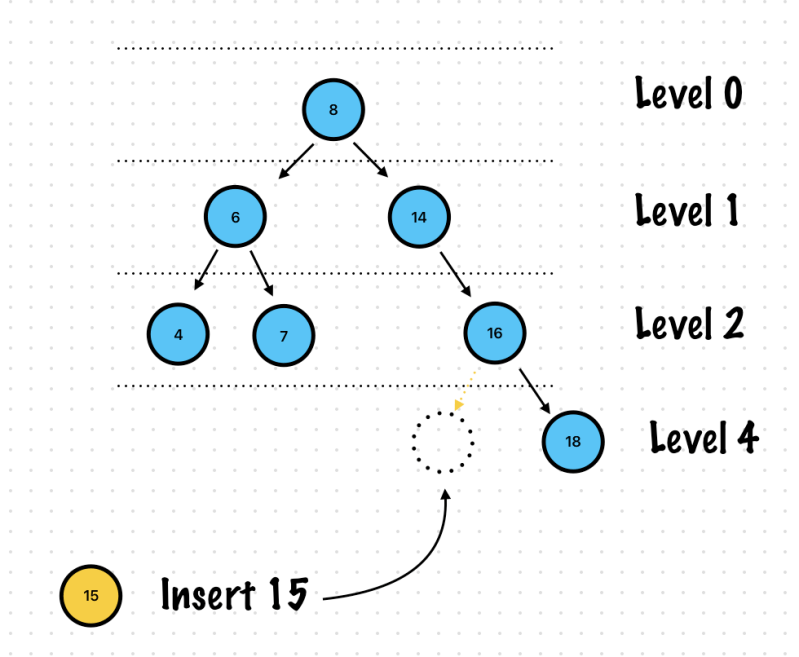
Let’s see step by step.
Step 1

Step 2
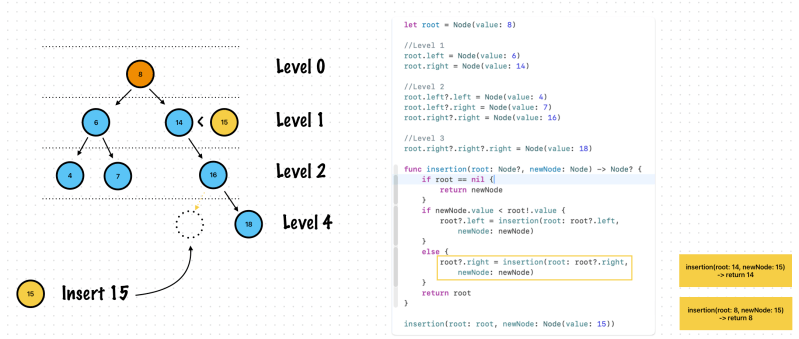
Step 3
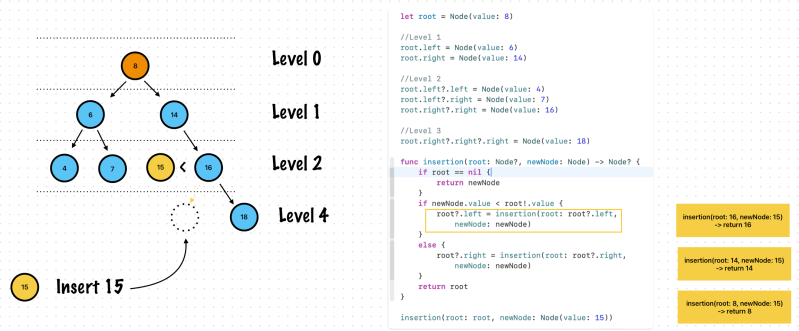
Step 4

Step 5

Step 6

Step 7

Step 8 -> Finish

class Node {
var left: Node?
var right: Node?
var value: Int
init(value: Int) {
self.value = value
}
}
let root = Node(value: 8)
//Level 1
root.left = Node(value: 6)
root.right = Node(value: 14)
//Level 2
root.left?.left = Node(value: 4)
root.left?.right = Node(value: 7)
root.right?.right = Node(value: 16)
//Level 3
root.right?.right?.right = Node(value: 18)
func insertion(root: Node?, newNode: Node) -> Node? {
if root == nil {
return newNode
}
if newNode.value < root!.value {
root?.left = insertion(root: root?.left, newNode: newNode)
}
else {
root?.right = insertion(root: root?.right, newNode: newNode)
}
return root
}
insertion(root: root, newNode: Node(value: 15))
func bfs(root: Node) {
var root = root
var queue = [Node]()
queue.append(root)
while !queue.isEmpty {
let dequeue = queue.removeFirst()
print("\(dequeue.value)", terminator: " ")
if let leftChild = dequeue.left {
queue.append(leftChild)
}
if let rightChild = dequeue.right {
queue.append(rightChild)
}
}
}
bfs(root: root)
//Prints
8 6 14 4 7 16 15 18
Look Up
You can consider 2 case. Found or Not Found
Found case
🙏 Below Images are wrong, Level 4 -> Level 3.
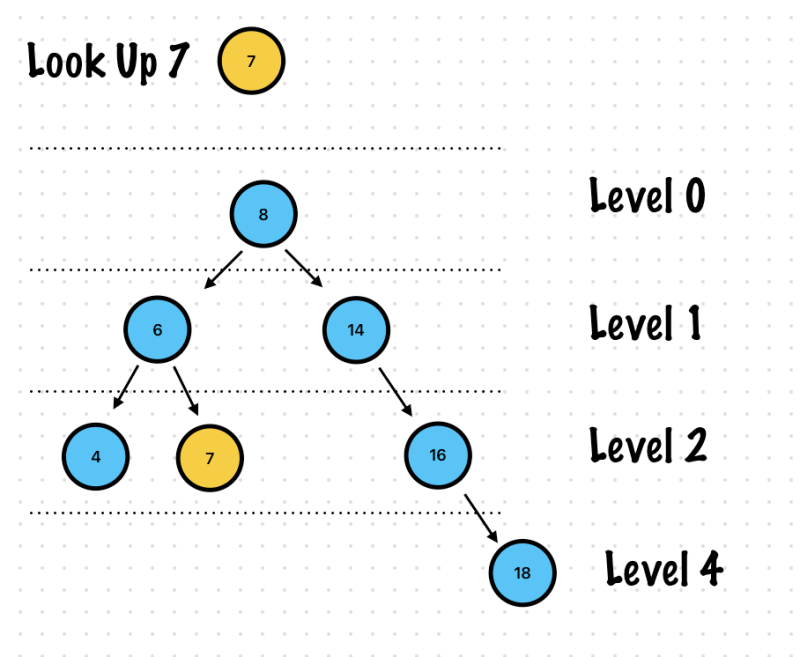
Not Found case
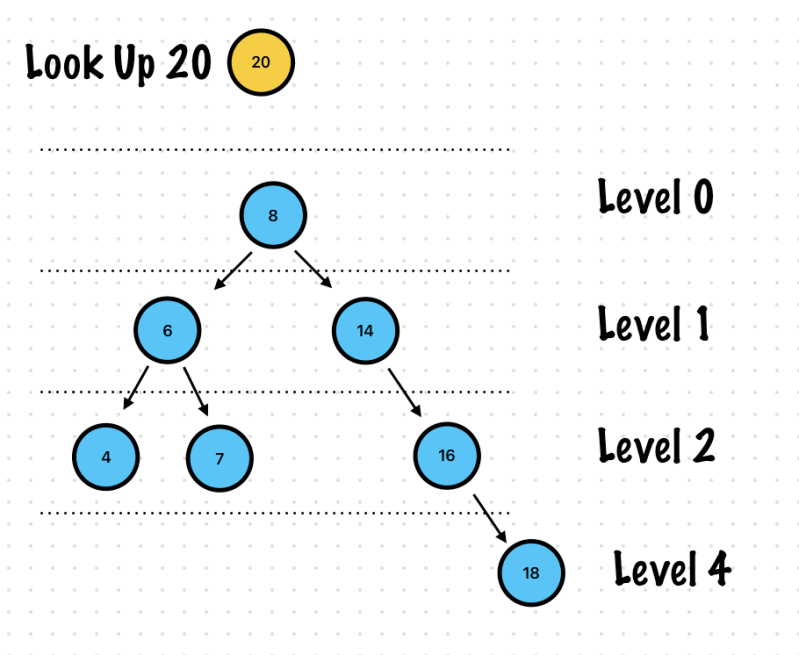
Let’s implement Look Up function
func lookUp(node: Node, from root: Node?) -> Node? {
if root == nil {
return nil
}
if node.value == root?.value {
return root
}
if node.value < root!.value {
return lookUp(node: node, from: root?.left)
}
else {
return lookUp(node: node, from: root?.right)
}
}
lookUp(node: Node(value: 7), from: root)?.value == 7 //found, true
lookUp(node: Node(value: 20), from: root)?.value == 20 //Not found, false
| Insertion | Look UP |
| Average complexity O(logN) | Average complexity O(logN) |
| The actual complexity depends on the shape of the tree – Skewed tree (I.E with all left or right children only) can have complexity of O(n) | For both insertion and lookup you halve the tree you have to traverse at every step. This gives us the O(logN) complexity |
Let’s practice. Binary Tree Problems
Exercise 1. Minimum Value
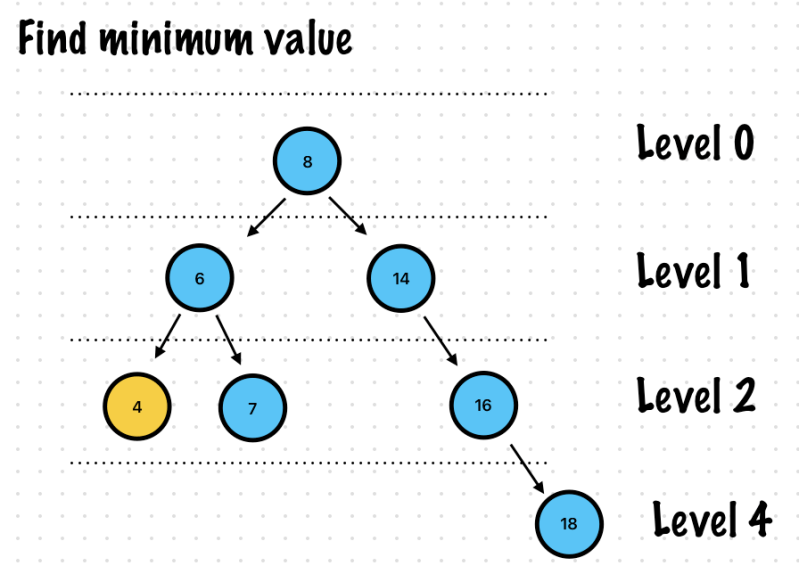
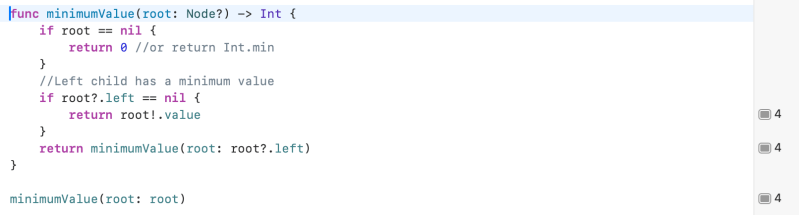
func minimumValue(root: Node?) -> Int {
if root == nil {
return 0 //or return Int.min
}
//Left child has a minimum value
if root?.left == nil {
return root!.value
}
return minimumValue(root: root?.left)
}
minimumValue(root: root)
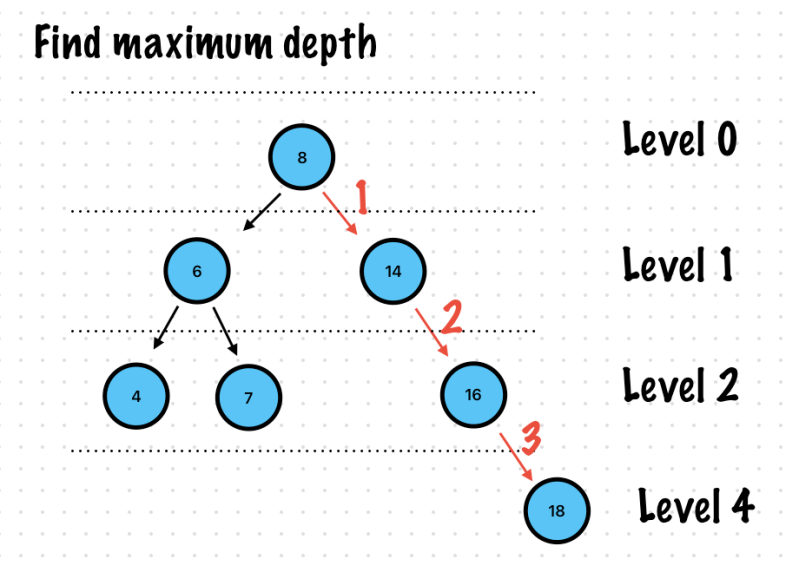
Exercise 2. Maximum Depth
🙏 Below Images are wrong, Level 4 -> Level 3.
func maximumDepth(root: Node?) -> Int {
if root == nil {
return 0
}
//Leaf node
if root?.left == nil, root?.right == nil {
return 0
}
//Count up when look up next level
let leftDepth = 1 + maximumDepth(root: root?.left)
let rightDepth = 1 + maximumDepth(root: root?.right)
return max(leftDepth, rightDepth)
}
maximumDepth(root: root) //Prints 3
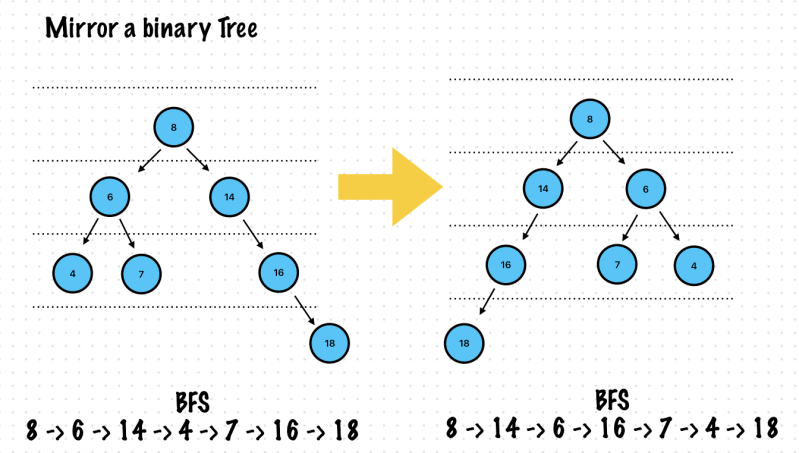
Exercise 3. Mirror Tree
func mirror(root: Node?) {
if root == nil {
return
}
mirror(root: root?.left)
mirror(root: root?.right)
//Switch left and right child
let temp = root?.left
root?.left = root?.right
root?.right = temp
}
mirror(root: root)

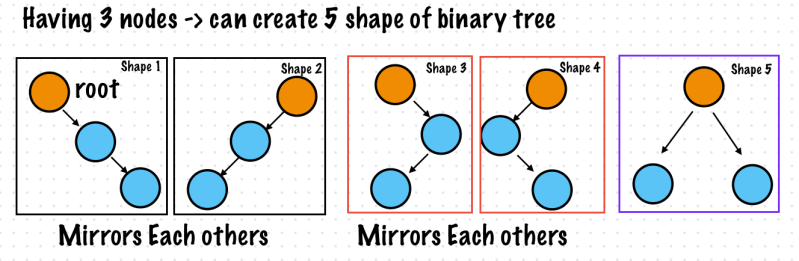
🤯 Exercise 4. Create the number of structurally unique Binary Trees possible
Problem definition
- Let say If you have 3 nodes, How many various binary trees you can create?
func countTrees(nodeCount: Int) -> Int {
//Base case: node 1 -> possible tree is 1, If it is zero then root node will be null
if nodeCount <= 1 {
return 1
}
var sum = 0
//Every node can be the root
for i in 1...nodeCount {
//Left and right form their own sub trees
//The nodes before it will be on the left
let leftTrees = countTrees(nodeCount: i - 1)
//THe nodes after it on the right
let rightTrees = countTrees(nodeCount: nodeCount - i)
//leftTree * rightTrees = the number of possible trees with this root
sum = sum + leftTrees * rightTrees
}
return sum
}
countTrees(nodeCount: 3) //Prints 5
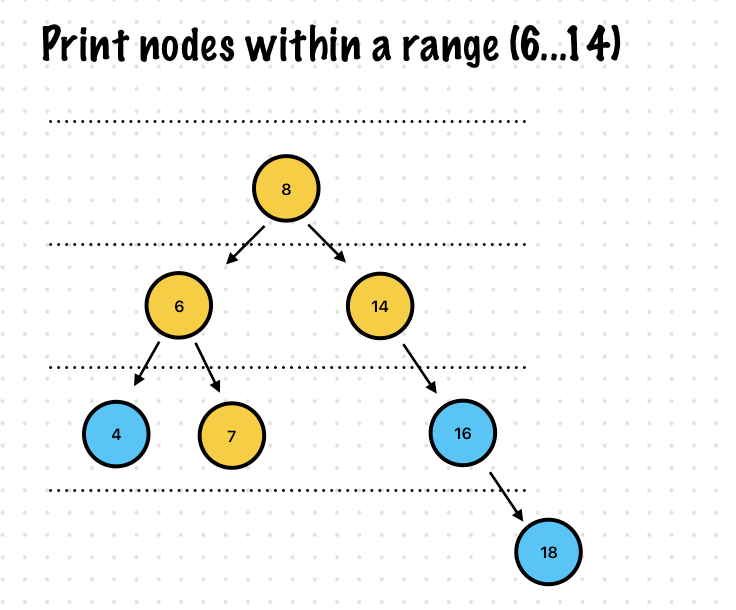
Exercise 5. Print all nodes within a range in a Binary Search Tree
func printAllNodeWithin(root: Node?, range: ClosedRange<Int>) {
if root == nil {
return
}
//If the range low value is less than the current, run the operation on the left subtree
if root!.value >= range.lowerBound {
printAllNodeWithin(root: root?.left, range: range)
}
//In-Order
if range ~= root!.value {
print("\(root!.value)", terminator: " ")
}
//If the range high value is greater than the current node, run the operation on the right subtree
if root!.value < range.upperBound {
printAllNodeWithin(root: root?.right, range: range)
}
}
print("\nExercise: Print All Nodes\n")
printAllNodeWithin(root: root, range: 6...14)
//Prints
Exercise: Print All Nodes
6 7 8 14
Exercise 6. Is a Binary Tree is a Binary Search Tree?
Remind what is Binary Search Tree?
- For every node in a binary search tree – The nodes with values <= node are in the left subtree and nodes with values > node are in the right sub tree

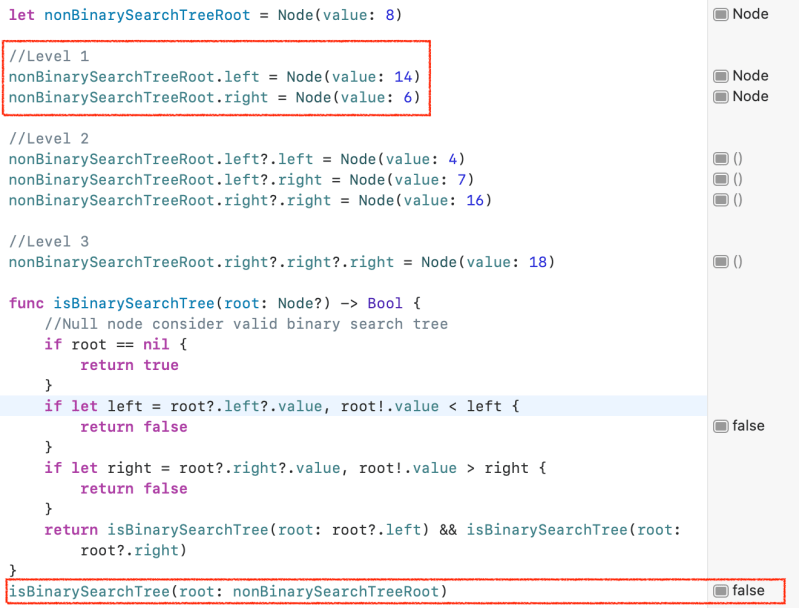
let nonBinarySearchTreeRoot = Node(value: 8)
//Level 1
nonBinarySearchTreeRoot.left = Node(value: 14)
nonBinarySearchTreeRoot.right = Node(value: 6)
//Level 2
nonBinarySearchTreeRoot.left?.left = Node(value: 4)
nonBinarySearchTreeRoot.left?.right = Node(value: 7)
nonBinarySearchTreeRoot.right?.right = Node(value: 16)
//Level 3
nonBinarySearchTreeRoot.right?.right?.right = Node(value: 18)
func isBinarySearchTree(root: Node?) -> Bool {
//Null node consider valid binary search tree
if root == nil {
return true
}
if let left = root?.left?.value, root!.value < left {
return false
}
if let right = root?.right?.value, root!.value > right {
return false
}
return isBinarySearchTree(root: root?.left) && isBinarySearchTree(root: root?.right)
}
isBinarySearchTree(root: nonBinarySearchTreeRoot) //Prints false
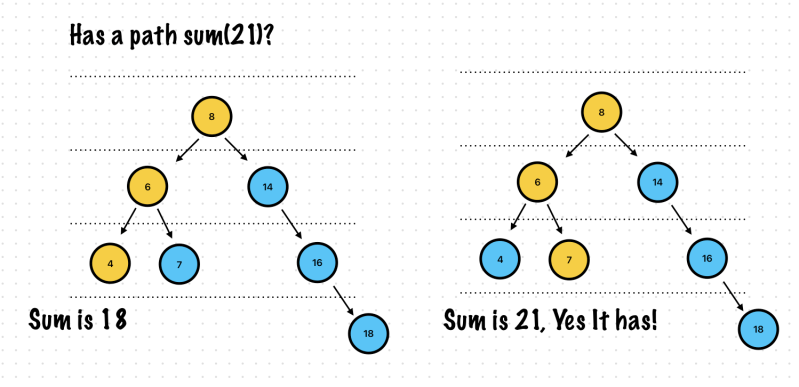
Exercise 7. Has Path Sum?
func hasPathSum(root: Node?, sum: Int) -> Bool {
//Check hasPathSum or not
if root?.left == nil, root?.right == nil {
return root?.value == sum
}
if root == nil {
return false
}
let subSum = sum - root!.value
if let left = root?.left {
var hasPathSum = hasPathSum(root: root?.left, sum: subSum)
if hasPathSum {
return true
}
}
if let right = root?.right {
var hasPassSum = hasPathSum(root: root?.right, sum: subSum)
if hasPassSum {
return true
}
}
return false
}
hasPathSum(root: root, sum: 21) //True
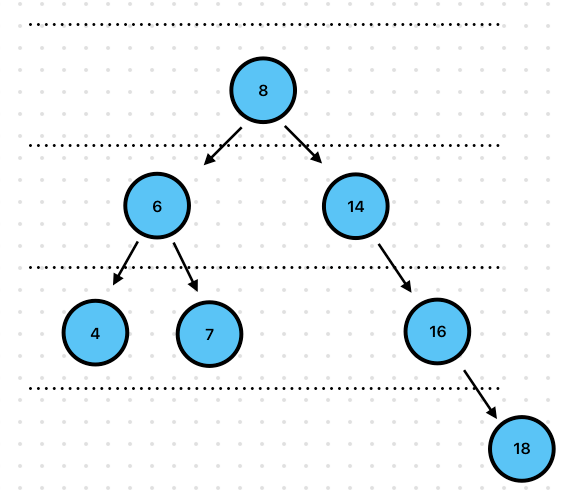
Exercise 8. Print Paths from Root -> Leaf node
func printAllPathes(root: Node?, array: inout [Int]) {
if root == nil {
return
}
array.append(root!.value)
printAllPathes(root: root?.left, array: &array)
printAllPathes(root: root?.right, array: &array)
if root?.left == nil, root?.right == nil {
print("Path: \(array)")
}
array.removeLast()
}
//Prints
Path: [8, 6, 4]
Path: [8, 6, 7]
Path: [8, 14, 16, 18]
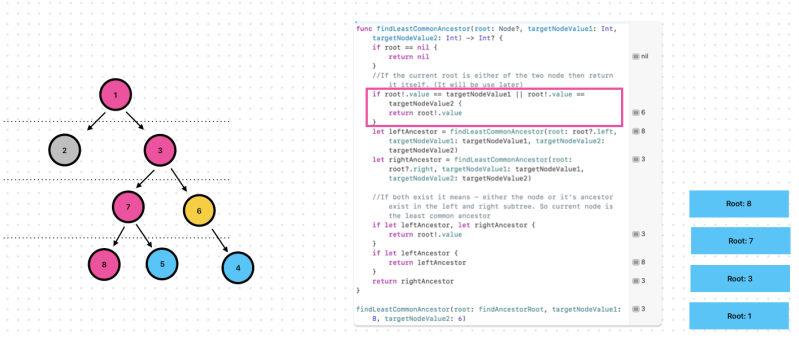
Exercise 9. Find the Least Common Ancestor for 2 nodes
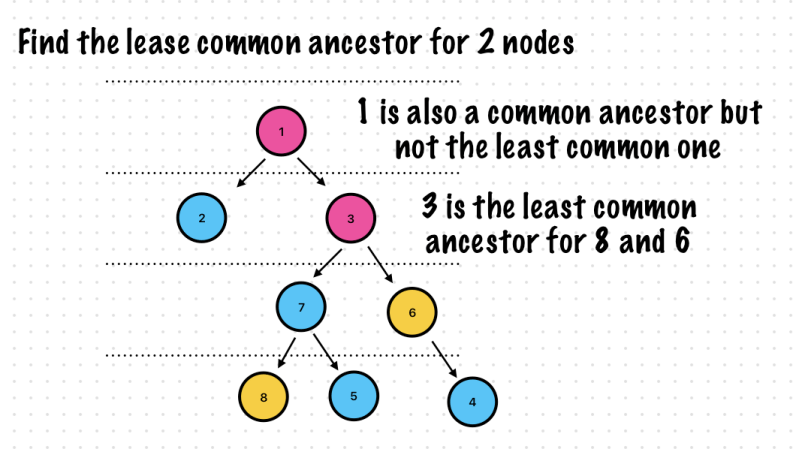
Let’s check step by step.

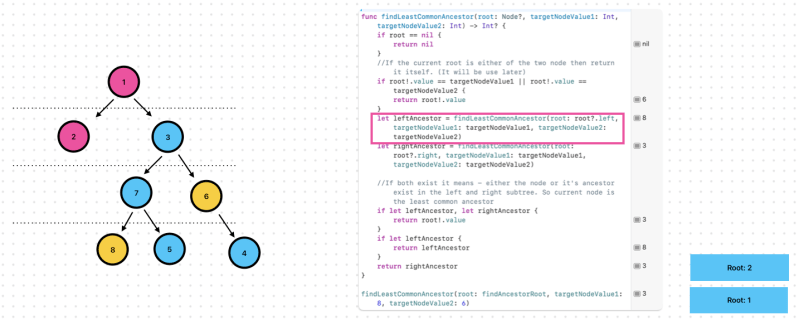
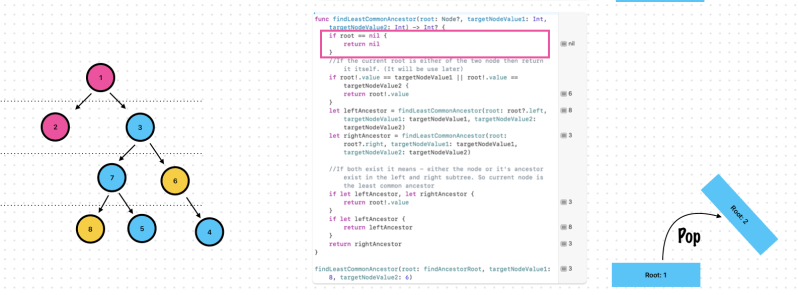
Remember, This step is important!


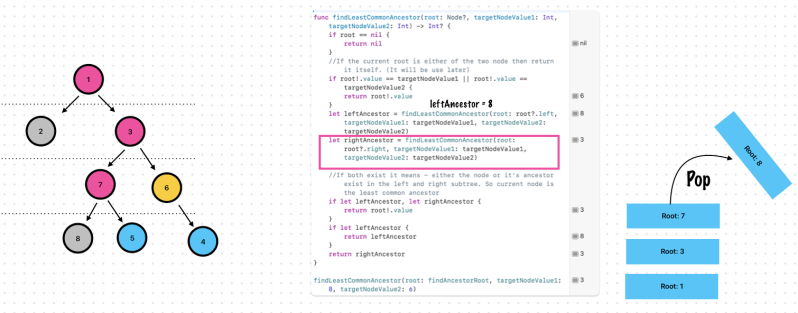


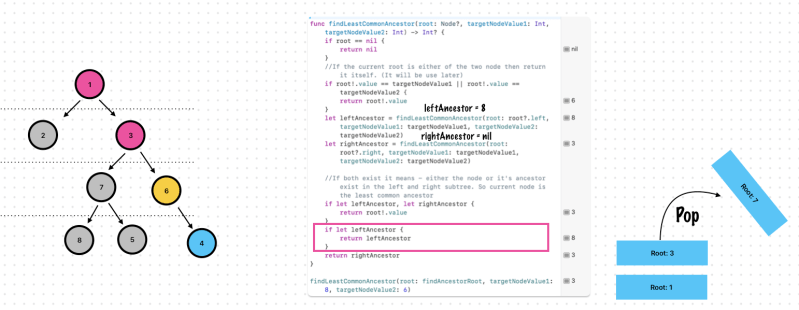
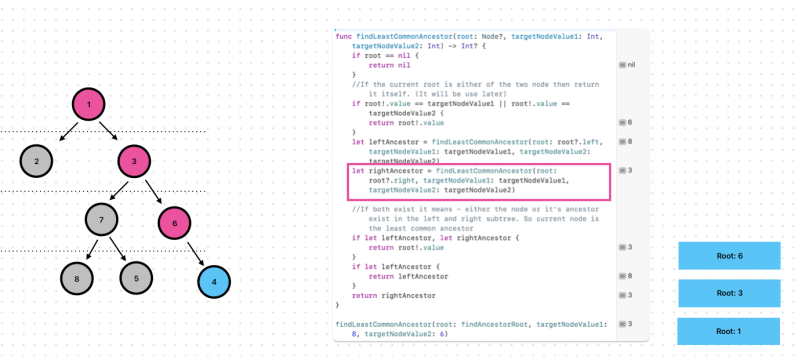
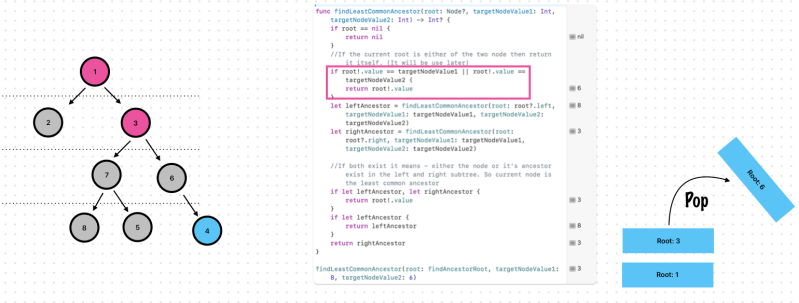

Found! The lease common ancestor is 3
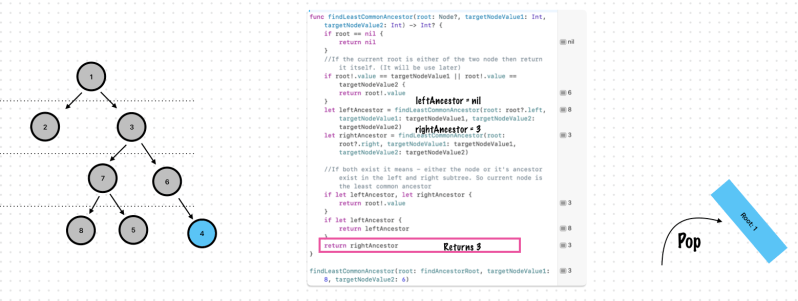
//It's not a Binary Search Tree
let findAncestorRoot = Node(value: 1)
//Level 1
findAncestorRoot.left = Node(value: 2)
findAncestorRoot.right = Node(value: 3)
//Level 2
findAncestorRoot.right?.left = Node(value: 7)
findAncestorRoot.right?.right = Node(value: 6)
//Level 3
findAncestorRoot.right?.left?.left = Node(value: 8)
findAncestorRoot.right?.left?.right = Node(value: 5)
findAncestorRoot.right?.right?.right = Node(value: 4)
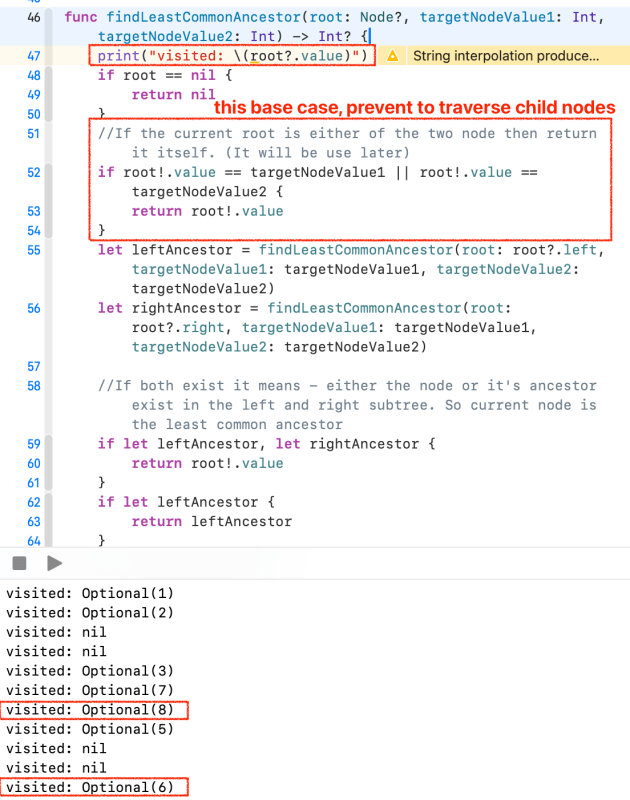
func findLeastCommonAncestor(root: Node?, targetNodeValue1: Int, targetNodeValue2: Int) -> Int? {
if root == nil {
return nil
}
//If the current root is either of the two node then return it itself. (It will be use later)
if root!.value == targetNodeValue1 || root!.value == targetNodeValue2 {
return root!.value
}
let leftAncestor = findLeastCommonAncestor(root: root?.left, targetNodeValue1: targetNodeValue1, targetNodeValue2: targetNodeValue2)
let rightAncestor = findLeastCommonAncestor(root: root?.right, targetNodeValue1: targetNodeValue1, targetNodeValue2: targetNodeValue2)
//If both exist it means - either the node or it's ancestor exist in the left and right subtree. So current node is the least common ancestor
if let leftAncestor, let rightAncestor {
return root!.value
}
if let leftAncestor {
return leftAncestor
}
return rightAncestor
}
findLeastCommonAncestor(root: findAncestorRoot, targetNodeValue1: 8, targetNodeValue2: 6) //It is 3
Exercise 10. iOS, Find the Least Common Ancestor for 2 subview
UIView is not a binary tree. It has more 2 child views.

func createNodeView(tag: Int) -> UIView {
let view = UIView()
view.tag = tag
return view
}
//Level 0
let rootView = createNodeView(tag: 1)
//Level 1
let tag3View = createNodeView(tag: 3)
rootView.addSubview(createNodeView(tag: 2))
rootView.addSubview(tag3View)
//Level 2
let tag7View = createNodeView(tag: 7)
let tag6View = createNodeView(tag: 6)
let tag9View = createNodeView(tag: 9)
tag3View.addSubview(tag7View)
tag3View.addSubview(tag6View)
tag3View.addSubview(tag9View)
//Level 3
tag7View.addSubview(createNodeView(tag: 11))
tag6View.addSubview(createNodeView(tag: 8))
tag6View.addSubview(createNodeView(tag: 5))
tag9View.addSubview(createNodeView(tag: 4))
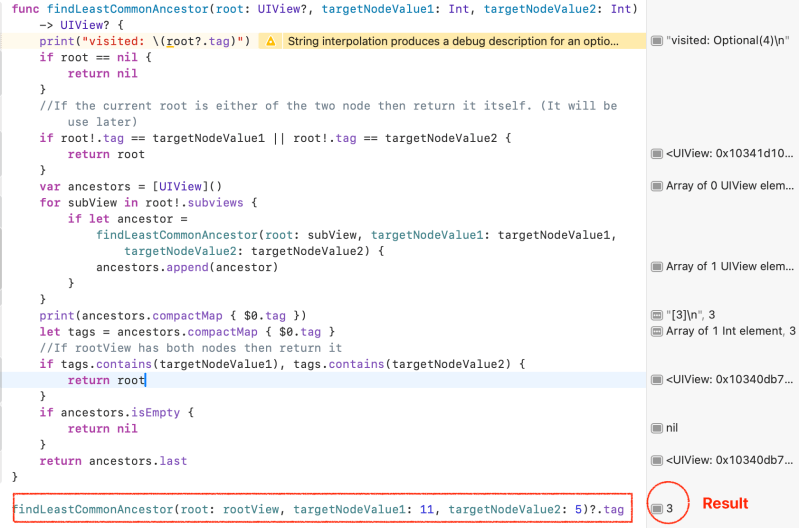
func findLeastCommonAncestor(root: UIView?, targetNodeValue1: Int, targetNodeValue2: Int) -> UIView? {
print("visited: \(root?.tag)")
if root == nil {
return nil
}
//If the current root is either of the two node then return it itself. (It will be use later)
if root!.tag == targetNodeValue1 || root!.tag == targetNodeValue2 {
return root
}
var ancestors = [UIView]()
for subView in root!.subviews {
if let ancestor =
findLeastCommonAncestor(root: subView, targetNodeValue1: targetNodeValue1, targetNodeValue2: targetNodeValue2) {
ancestors.append(ancestor)
}
}
print(ancestors.compactMap { $0.tag })
let tags = ancestors.compactMap { $0.tag }
//If rootView has both nodes then return it
if tags.contains(targetNodeValue1), tags.contains(targetNodeValue2) {
return root
}
if ancestors.isEmpty {
return nil
}
//Need to check whether It's okay to return last item or not..but most of cases It works correctly so far.
return ancestors.last
}

Leave a reply to iOS, Find least common ancestor from 2 UIViews – Shawn Cancel reply