✍️ Note
Some codes and contents are sourced from Udemy. This post is for personal notes where I summarize the original contents to grasp the key concepts (🎨 some images I draw it)
Graph
A graph is used to represent relationships between entities
Graphs are used to represent information in many many real world applications
Graphs are also favorite interview questions – They can start from simple concepts and get arbitrarily complex
Graph theory is a complex field of study by itself – There are many algorithms to optimize different problems represented using graphs
First principle of graph can solve most of the graph problems
Vertex
- The entities can be anything – Graphs find applications in variety of ways in the real word
Edge
- These relationships can be arbitrarily complicated and of a variety of different types
Real word Example
- LinkedIn (Professional Graph)
- Entities: People
- Edge: Professional relationships – people work together
- Facebook (Social Graph)
- Entities: People
- Edge: Personal relationships – People are friends
- GoogleMaps (Locations)
- Entities: Locations
- Edge: A way to get from one location to another – Roads, Rail, Air
- Each of these can be further thought of in terms of specific means of transport
- Bus, Car, Taxi, Individual trains, Airlines
- at&t (Phone network)
- Entities: Old fashioned phones – landlines
- Edge: A network to carry voice from one instrument to another
- cisco / google and more (Internet)
- Entities: Computers across the world
- Edge: A way to send information or data from one computer to another
- This can information can be routed wirelessly or over wires
https://www.udemy.com/course/break-away-coding-interviews-1/learn/lecture/8474120#content
What is a graph?
A graph is a set of vertices and edges (V, E)
- A very simple graph is one vertex
- Two vertices and a single edge is also a valid graph
https://www.udemy.com/course/break-away-coding-interviews-1/learn/lecture/8484198#content
Undirected Graph
Undirected Graph
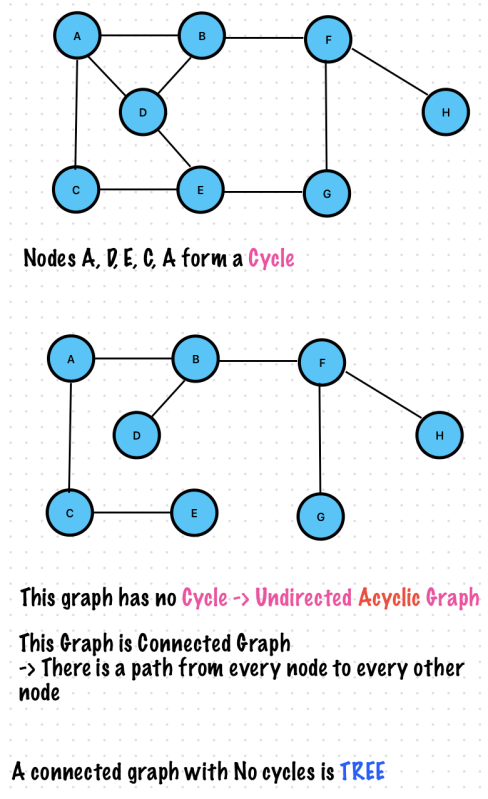
Unconnected Graph
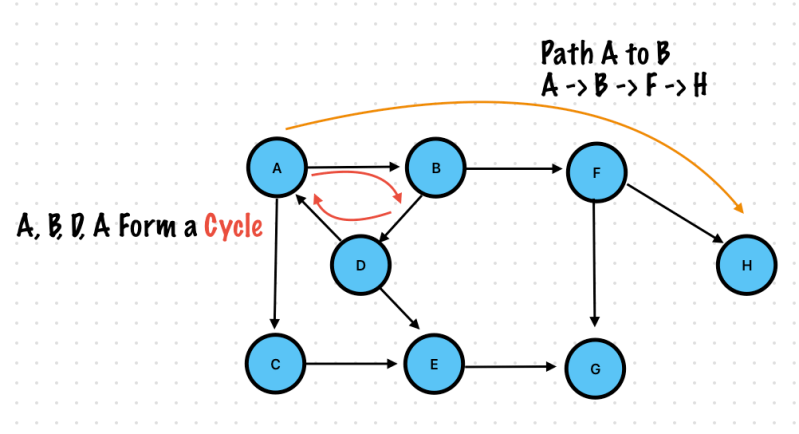
Directed Graph
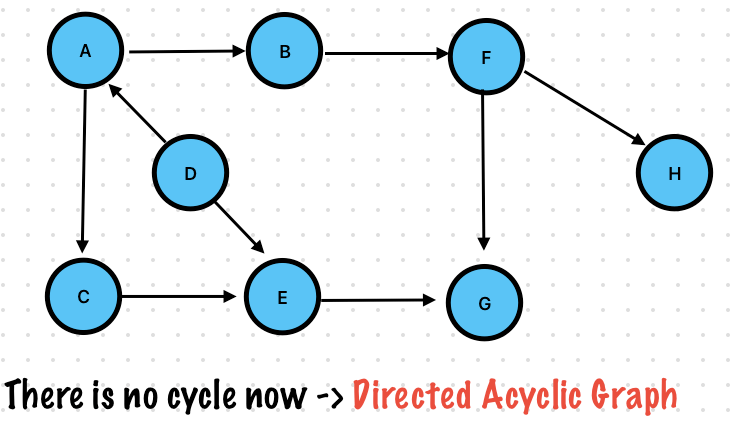
Directed Acyclic Graph
Graph Representation
A way to model a vertex which may hold some information
A way to model directed or undirected edges
There are 3 standard ways that graphs can be represented
- Adjacency Matrix
- Adjacency List
- Adjacency Set
https://www.udemy.com/course/break-away-coding-interviews-1/learn/lecture/8474130#content
Graph Interface
enum GraphType {
case directed
case undirected
}
protocol Graph {
func addEdge(src: Int, dst: Int)
//Helper to get the adjacent vertices for any vertex - A method which is required for all algorithms involving graphs
func getAdjacentVertices(vertext: Int) -> [Int]?
}
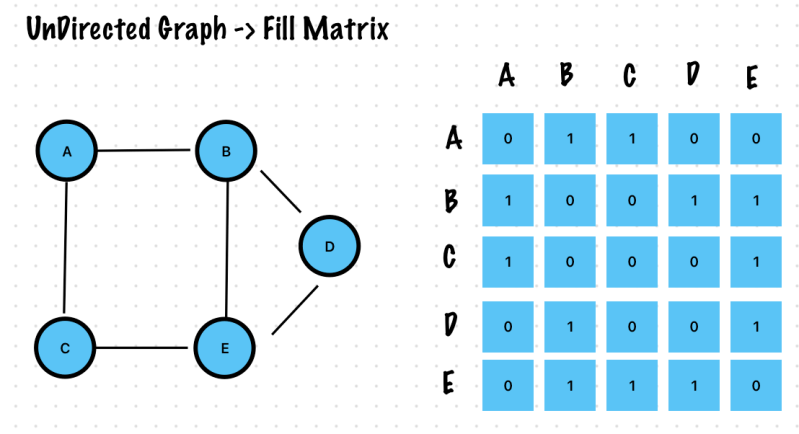
Adjacency Matrix
Use A Matrix with Rows and Columns – It just a Table
The row labels and the column labels represent the vertices
Each cell represents the relationship between the vertices. I.E. The edges
https://www.udemy.com/course/break-away-coding-interviews-1/learn/lecture/8474136#content
enum GraphType {
case directed
case undirected
}
protocol Graph {
func addEdge(src: Int, dst: Int)
func getAdjacentVertices(vertext: Int) -> [Int]?
}
class AdjacencyMatrix: Graph {
private var matrix: [[Int]]
private let type: GraphType
init(vertices: [Int], graphType: GraphType) {
matrix = Array(
repeating: Array(
repeating: 0,
count: vertices.count
), count: vertices.count
)
type = graphType
}
func addEdge(src: Int, dst: Int) {
let range = 0..<matrix[0].count
guard range ~= src, range ~= dst else {
return
}
matrix[src][dst] = 1
if type == .undirected {
matrix[dst][src] = 1
}
}
func getAdjacentVertices(vertext: Int) -> [Int]? {
let range = 0..<matrix[0].count
guard range ~= vertext else {
return nil
}
var result = [Int]()
for i in 0..<matrix[0].count {
//If 1 is present in the cell it means that the vertext V is directly connected to another vertex
if matrix[vertext][i] == 1 {
result.append(i)
}
}
//Always return the vertices in ascending order - to compare with other values's adjacents
return result.sorted(by: { $0 < $1 })
}
}
Adjacency List
Each vertex is a node
Each vertex has a pointer to a linked list
This linked list contains all the other nodes this vertex connects to directly
If a vertex V has an edge leading to another vertex U
The U is present in V’s linked list
https://www.udemy.com/course/break-away-coding-interviews-1/learn/lecture/8474138#content
Directed Graph – Adjacency List
I’ll skip implementation of adjacency list. Use 2D Matrix or Set, It’s the simple and easy to handle logics.
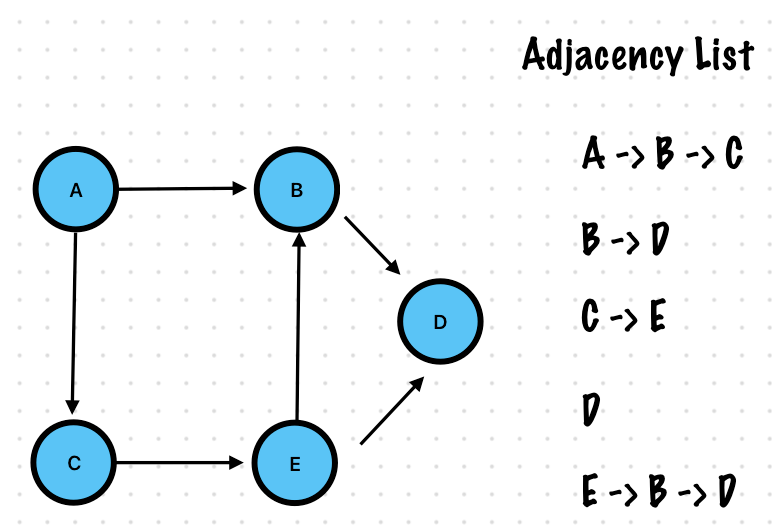
Cons
- Order of the vertices in the adjacency lists matter
- The same graph can have multiple representations
Certain operations become tricky. E.G. Deleting a node involves looking through all the adjacency lists to remove the node from all lists
https://www.udemy.com/course/break-away-coding-interviews-1/learn/lecture/8474138#content
Adjacency Set
This is very similar to an adjacency list
Instead of a linked list to maintain the adjacent vertices It use a Set
https://www.udemy.com/course/break-away-coding-interviews-1/learn/lecture/8474138#content
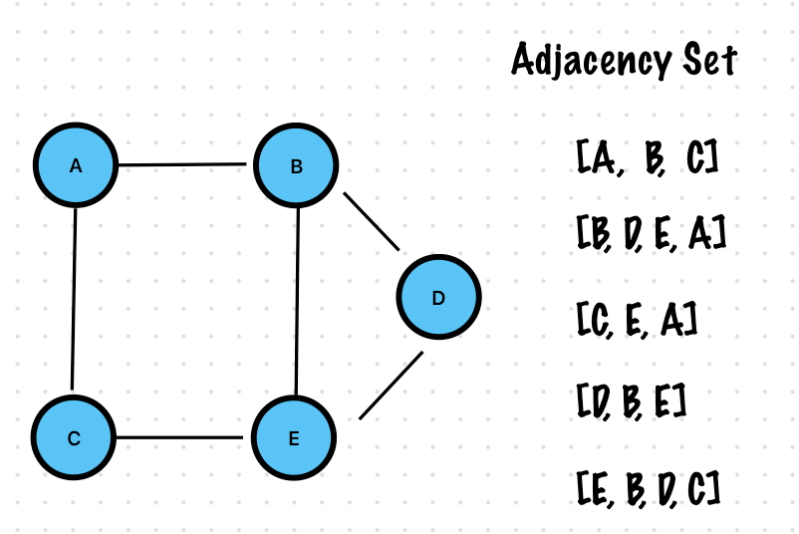
enum GraphType {
case directed
case undirected
}
protocol Graph {
func addEdge(src: Int, dst: Int)
func getAdjacentVertices(vertext: Int) -> [Int]?
}
class Vertex {
let value: Int
var adjacencySet: Set<Int>
init(value: Int, adjacencySet: Set<Int>) {
self.value = value
self.adjacencySet = adjacencySet
}
func addEdge(vertext: Int) {
adjacencySet.insert(vertext)
}
func getAdjacentVertices() -> [Int] {
let array = Array(adjacencySet)
return array.sorted(by: { $0 < $1 })
}
}
class GraphAdjacencySet: Graph {
var vertices: [Vertex]
let graphType: GraphType
var numberOfVertice = 0
init(numberOfVertices: Int, graphType: GraphType) {
self.vertices = [Vertex]()
for i in 0..<numberOfVertices {
vertices.append(Vertex(value: i, adjacencySet: []))
}
self.numberOfVertice = numberOfVertices
self.graphType = graphType
}
func addEdge(src: Int, dst: Int) {
let range = 0..<numberOfVertice
guard range ~= src, range ~= dst else {
return
}
vertices[src].addEdge(vertext: dst)
if graphType == .undirected {
vertices[dst].addEdge(vertext: src)
}
}
func getAdjacentVertices(vertext: Int) -> [Int]? {
let range = 0..<numberOfVertice
guard range ~= vertext else {
return nil
}
return vertices[vertext].getAdjacentVertices()
}
}
Comparison of Graph Representations
Adjacency Matrix
- This works well when the graph is well connected I.E. Many nodes are connected with many other nodes
- The overhead of V^2 space is worth it when the number of connections are large.
Adjacency List/Set
- A Sparse graph with few connections between nodes might be more efficiently represented using adjacency list or set
E = Number of Edges
V = Number of Vertices
Space
- Adjacency Matrix -> O(V^2)
- Adjacency List -> O(E + V)
- Adjacency Set -> O(E + V)
Is Edge Present
- Adjacency Matrix -> O(1), look up in 2D Array
- Adjacency List -> Degree of V
- Adjacency Set -> O(LogDegree of V) <- like a binary search…
Iterate over edges on a vertex
- Adjacency Matrix -> O(V)
- Adjacency List -> Degree of V
- Adjacency Set -> Degree of V
https://www.udemy.com/course/break-away-coding-interviews-1/learn/lecture/8474144#content
Graph Traversal
This is very similar to tree traversal
Depth-First
Breadth-First
One additional wrinkle
- In A Tree there is only one path from the root to a specific node
- In A Graph multiple paths can lead from one node to another
- A Graph can also have cycles, so the same node can be visited multiple times
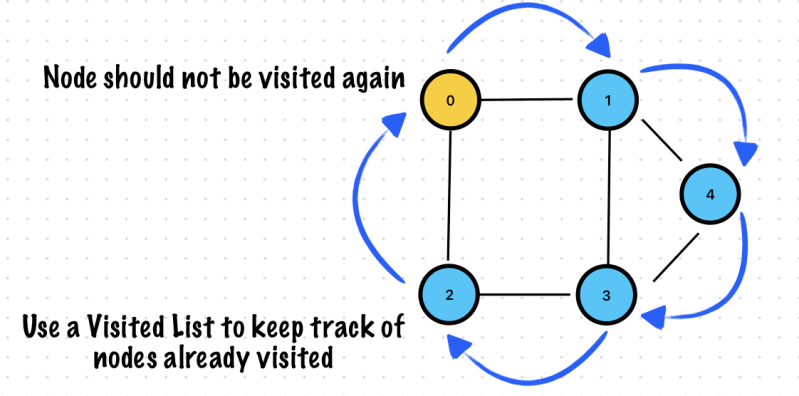
In order to avoid infinite looping in a graph we need to keep track of the nodes previously visited
https://www.udemy.com/course/break-away-coding-interviews-1/learn/lecture/8474146#content
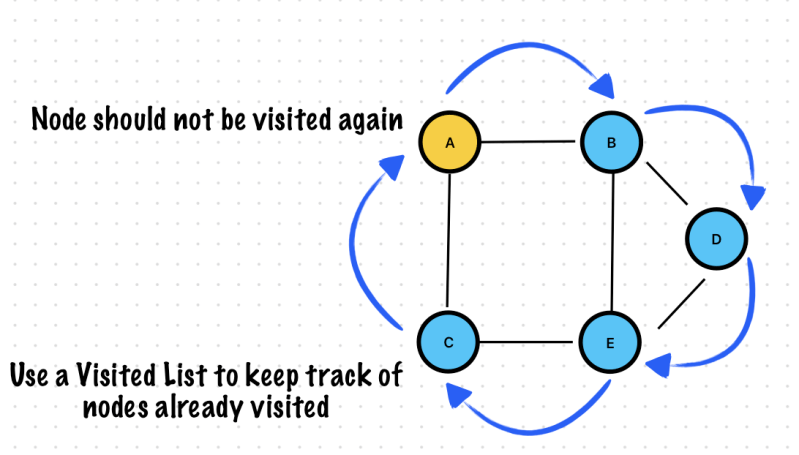
Depth First Traversal
//Vertex is 5
var visited = Array(repeating: 0, count: 5)
func dfsGraph(graph: Graph, visited: inout [Int], currentVertex: Int) {
if visited[currentVertex] == 1 {
return
}
visited[currentVertex] = 1
let list = graph.getAdjacentVertices(vertext: currentVertex) ?? []
for v in list {
dfsGraph(graph: graph, visited: &visited, currentVertex: v)
}
//This for loop ensures that all nodes are covered even for an unconnected graph
for i in 0..<visited.count {
dfsGraph(graph: graph, visited: &visited, currentVertex: i)
}
//Post order Traversal
print("\(currentVertex)", terminator: "->")
}
let graph = AdjacencyMatrix(vertices: [0, 1, 2, 3, 4], graphType: .undirected)
graph.addEdge(src: 0, dst: 1)
graph.addEdge(src: 0, dst: 2)
graph.addEdge(src: 1, dst: 4)
graph.addEdge(src: 1, dst: 3)
graph.addEdge(src: 1, dst: 0)
graph.addEdge(src: 2, dst: 0)
graph.addEdge(src: 2, dst: 3)
graph.addEdge(src: 3, dst: 2)
graph.addEdge(src: 3, dst: 1)
graph.addEdge(src: 3, dst: 4)
graph.addEdge(src: 4, dst: 1)
graph.addEdge(src: 4, dst: 3)
dfsGraph(graph: graph, visited: &visited, currentVertex: 0)
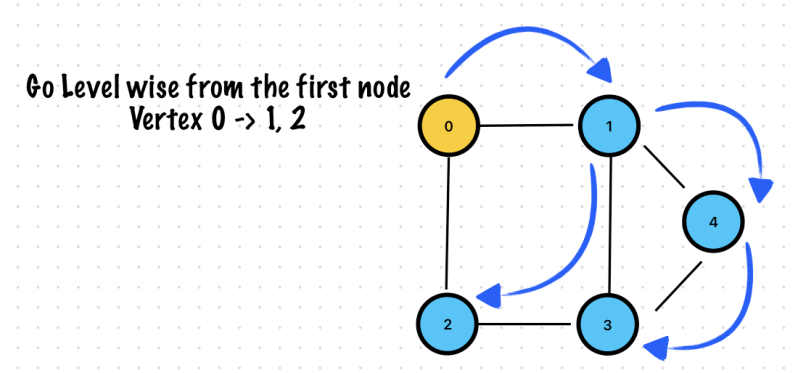
Breadth First Traversal
Go level wise from the first node
Add non-visited child nodes to a queue
Visited = true means the node has been seen before
Use a visited list to keep track of nodes already visited
Not using recursive call
https://www.udemy.com/course/break-away-coding-interviews-1/learn/lecture/8474146#content
func bfsGraph(graph: Graph, visited: inout [Int], currentVertext: Int) {
var queue = [Int]()
queue.append(currentVertext)
while !queue.isEmpty {
let vertex = queue.removeFirst()
if visited[vertex] == 1 {
continue
}
print("\(vertex)", terminator: "->")
//MARK Visited
visited[vertex] = 1
if let adjacentVertices = graph.getAdjacentVertices(vertext: vertex) {
for v in adjacentVertices {
if visited[v] != 1 {
queue.append(v)
}
}
}
}
}
let graph = AdjacencyMatrix(vertices: [0, 1, 2, 3, 4], graphType: .undirected)
graph.addEdge(src: 0, dst: 1)
graph.addEdge(src: 0, dst: 2)
graph.addEdge(src: 1, dst: 4)
graph.addEdge(src: 1, dst: 3)
graph.addEdge(src: 1, dst: 0)
graph.addEdge(src: 2, dst: 0)
graph.addEdge(src: 2, dst: 3)
graph.addEdge(src: 3, dst: 2)
graph.addEdge(src: 3, dst: 1)
graph.addEdge(src: 3, dst: 4)
graph.addEdge(src: 4, dst: 1)
graph.addEdge(src: 4, dst: 3)
bfsGraph(graph: graph, visited: &visited, currentVertext: 0)
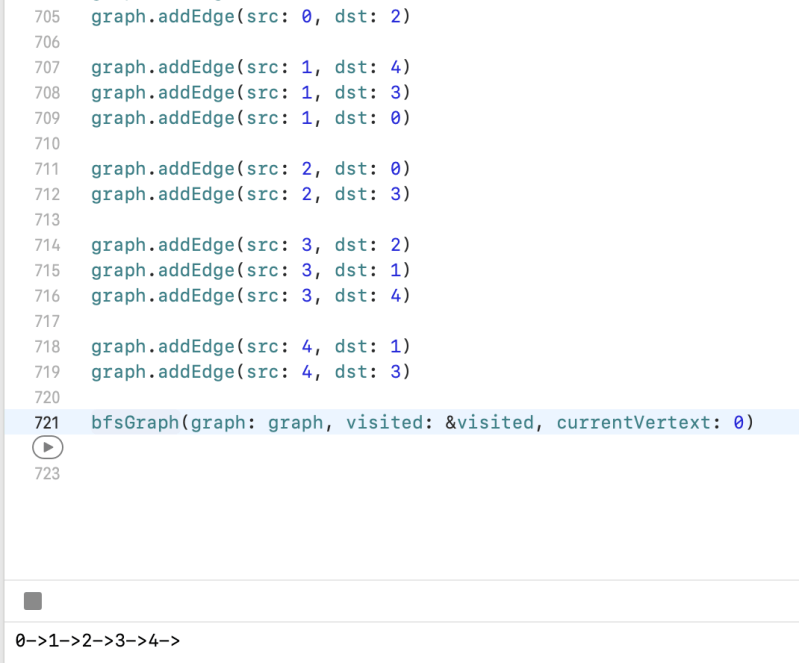
Check Unconnected Graph – BFS
🔥 BFS is not using a recursive call. Don’t put below logic inside bfsGraph function!
//This for loop ensures that all nodes are covered even for an unconnected graph
for i in 0..<visited.count {
bfsGraph(graph: graph, visited: &visited, currentVertext: i)
}
Exercise 1. Topological Sort
It is an ordering of vertices in a directed acyclic graph in which each node comes before all the nodes to which
It has outgoing edges
A -> B
- A should come before B
https://www.udemy.com/course/break-away-coding-interviews-1/learn/lecture/8474156#content
Find first vertex
If there are vertices which has no incoming edge, you can start any of vertex among them.
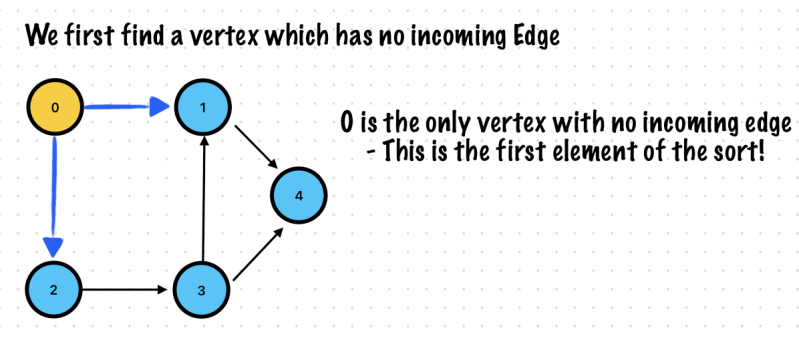
Indegree
- Number of inward directed graph edges for a given graph vertex
- Indegree of vertex 0 is 0
If there were no vertices with 0 indegree, then there would have been no topological sort -> The graph has a cycle.
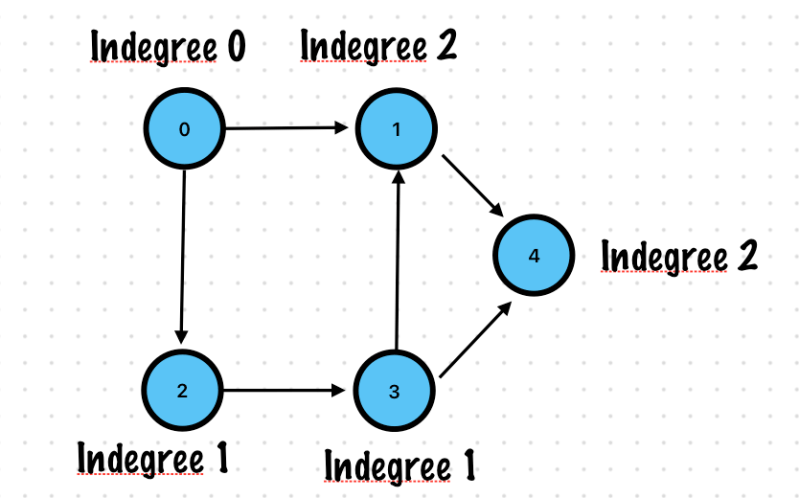
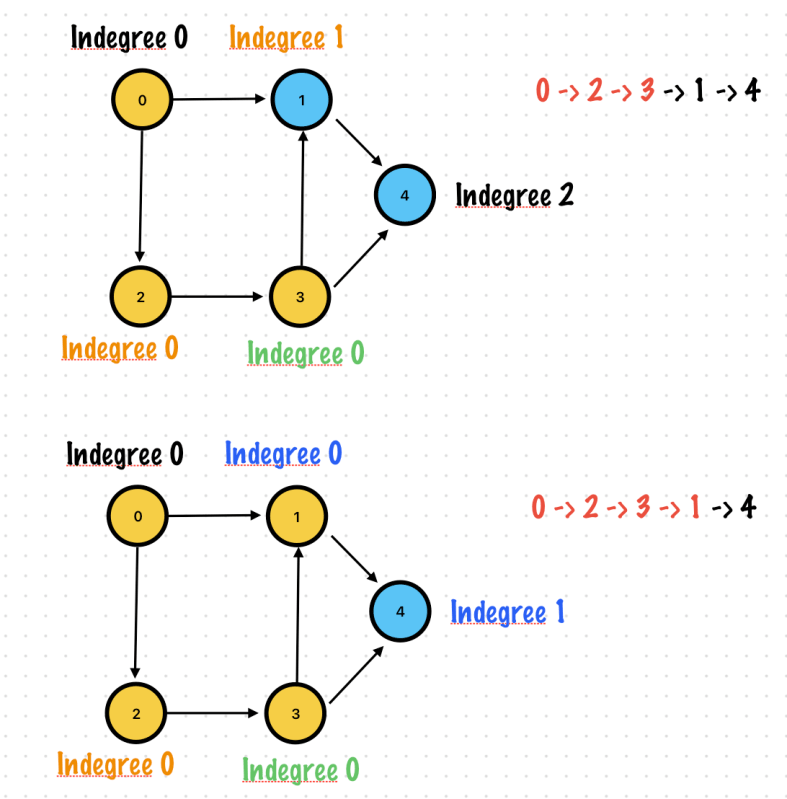
It is an ordering of vertices in a Directed Acyclic Graph in which each node comes before all the nodes to which. It has outgoing edges
Final code for topological sort. (I added 2 functions)
enum GraphType {
case directed
case undirected
}
protocol Graph {
func addEdge(src: Int, dst: Int)
func getAdjacentVertices(vertext: Int) -> [Int]?
//New functions
func getIndegree(vertext: Int) -> Int
var numberOfVertices: Int { get set }
}
class Vertex {
let value: Int
var adjacencySet: Set<Int>
init(value: Int, adjacencySet: Set<Int>) {
self.value = value
self.adjacencySet = adjacencySet
}
func addEdge(vertext: Int) {
adjacencySet.insert(vertext)
}
func getAdjacentVertices() -> [Int] {
let array = Array(adjacencySet)
return array.sorted(by: { $0 < $1 })
}
}
Using Matrix
class AdjacencyMatrix: Graph {
var numberOfVertices: Int
private var matrix: [[Int]]
private let type: GraphType
init(vertices: [Int], graphType: GraphType) {
matrix = Array(
repeating: Array(
repeating: 0,
count: vertices.count
), count: vertices.count
)
numberOfVertices = vertices.count
type = graphType
}
func addEdge(src: Int, dst: Int) {
let range = 0..<numberOfVertices
guard range ~= src, range ~= dst else {
return
}
matrix[src][dst] = 1
if type == .undirected {
matrix[dst][src] = 1
}
}
func getAdjacentVertices(vertext: Int) -> [Int]? {
let range = 0..<numberOfVertices
guard range ~= vertext else {
return nil
}
var result = [Int]()
for i in 0..<numberOfVertices {
//If 1 is present in the cell it means that the vertext V is directly connected to another vertex
if matrix[vertext][i] == 1 {
result.append(i)
}
}
//Always return the vertices in ascending order - to compare with other values's adjacents
return result.sorted(by: { $0 < $1 })
}
//New function, Get Indegree of vertex
func getIndegree(vertext: Int) -> Int {
let range = 0..<numberOfVertices
guard range ~= vertext else {
return 0
}
var indegree = 0
//Loop from 0 to all vertex
for i in 0..<numberOfVertices {
//src = i, dst = vertex
if matrix[i][vertext] != 0 {
indegree += 1
}
}
return indegree
}
}
Topological Sort
func topologicalSort(graph: Graph) -> [Int] {
var queue = [Int]()
var indgreeMap = [Int: Int]()
//Step 1. Add first node of sort
for i in 0..<graph.numberOfVertices {
let indegree = graph.getIndegree(vertext: i)
//Add indegree 0's vertex to queue
indgreeMap[i] = indegree
//Add all vertices with indegree = 0 to the queue of vertices to explore
if indegree == 0 {
queue.append(i)
}
}
print(indgreeMap)
var result = [Int]()
//BFS
while !queue.isEmpty {
let vertex = queue.removeLast()
result.append(vertex)
var adjacentVertices = graph.getAdjacentVertices(vertext: vertex) ?? []
print("v: \(vertex) -> neighbors: \(adjacentVertices)")
for v in adjacentVertices {
//Important! get indegree from dictionary!
//Get the adjacent vertices of the current one and decrement their indegrees by 1
let updatedIndegree = indgreeMap[v]! - 1
indgreeMap[v] = updatedIndegree
//For every vertex which now has indegree = 0, It's a potential next node for the topological sort
if updatedIndegree == 0 {
queue.append(v)
}
}
}
print(result)
//If the final sorted list is not same to the number of vertices in the graph there is a cycles
if result.count != graph.numberOfVertices {
print("There is cycle")
return []
}
return result
}
Topological sort using Matrix
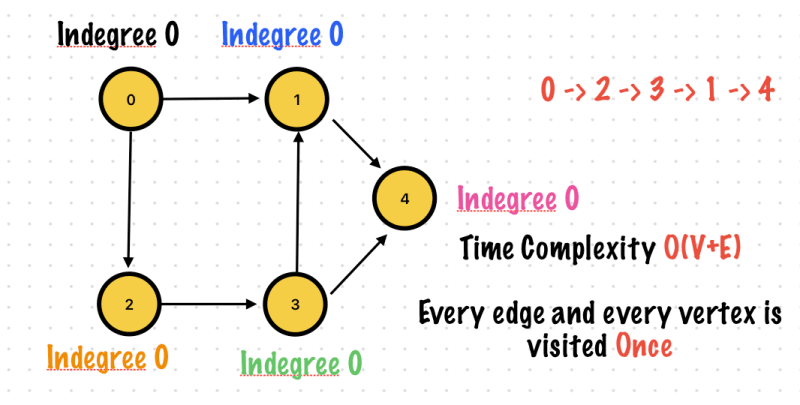
let graph = AdjacencyMatrix(vertices: [0, 1, 2, 3, 4], graphType: .directed) graph.addEdge(src: 0, dst: 1) graph.addEdge(src: 0, dst: 2) graph.addEdge(src: 1, dst: 4) graph.addEdge(src: 2, dst: 3) graph.addEdge(src: 3, dst: 1) graph.addEdge(src: 3, dst: 4) topologicalSort(graph: graph)
Using Set
class GraphAdjacencySet: Graph {
var vertices: [Vertex]
let graphType: GraphType
var numberOfVertices: Int
init(numberOfVertices: Int, graphType: GraphType) {
self.vertices = [Vertex]()
for i in 0..<numberOfVertices {
vertices.append(Vertex(value: i, adjacencySet: []))
}
self.numberOfVertices = numberOfVertices
self.graphType = graphType
}
func addEdge(src: Int, dst: Int) {
let range = 0..<numberOfVertices
guard range ~= src, range ~= dst else {
return
}
vertices[src].addEdge(vertext: dst)
if graphType == .undirected {
vertices[dst].addEdge(vertext: src)
}
}
func getAdjacentVertices(vertext: Int) -> [Int]? {
let range = 0..<numberOfVertices
guard range ~= vertext else {
return nil
}
return vertices[vertext].getAdjacentVertices()
}
//New function, Get Indegree of vertex
func getIndegree(vertext: Int) -> Int {
let range = 0..<numberOfVertices
guard range ~= vertext else {
return 0
}
var indegree = 0
//Loop from 0 to all vertex
for i in 0..<numberOfVertices {
if getAdjacentVertices(vertext: i)?.contains(vertext) == true {
indegree += 1
}
}
return indegree
}
}
let graph = GraphAdjacencySet(numberOfVertices: 5, graphType: .directed) graph.addEdge(src: 0, dst: 1) graph.addEdge(src: 0, dst: 2) graph.addEdge(src: 1, dst: 4) graph.addEdge(src: 2, dst: 3) graph.addEdge(src: 3, dst: 1) graph.addEdge(src: 3, dst: 4) topologicalSort(graph: graph)
As you can see the results are the same. You don’t need to change topological sort logic, Because both Set and Matrix implements Graph interface.
Exercise 2. Design A Course Schedule Considering Pre-reqs for Courses
Design a schedule for a student to complete her degree given the list of courses along with the prerequisites for each course
We have 2 lists
- List of courses
- List of pre-reqs for each course
This contains pairs (course A, course B) where course A, course B belong to courses list and course A should be taken before course B
We want to know a valid order in which the student can take her courses!
https://www.udemy.com/course/break-away-coding-interviews-1/learn/lecture/8474160#content
Each course can be a vertex
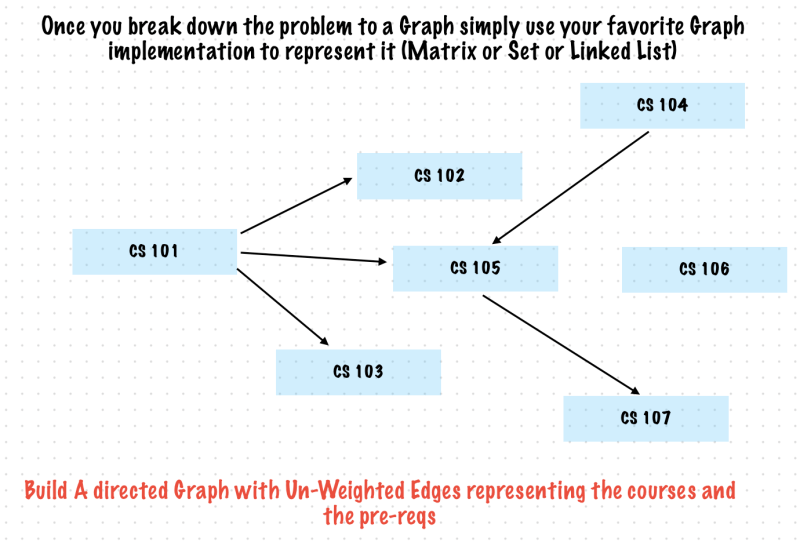
Any course that has pre-reqs should not come before its pre-reqs in the schedule!
It is an ordering of vertices in a directed acyclic graph in which each node comes before all the nodes to which it has outgoing edges
It’s a Topological Sort!
https://www.udemy.com/course/break-away-coding-interviews-1/learn/lecture/8474160#content
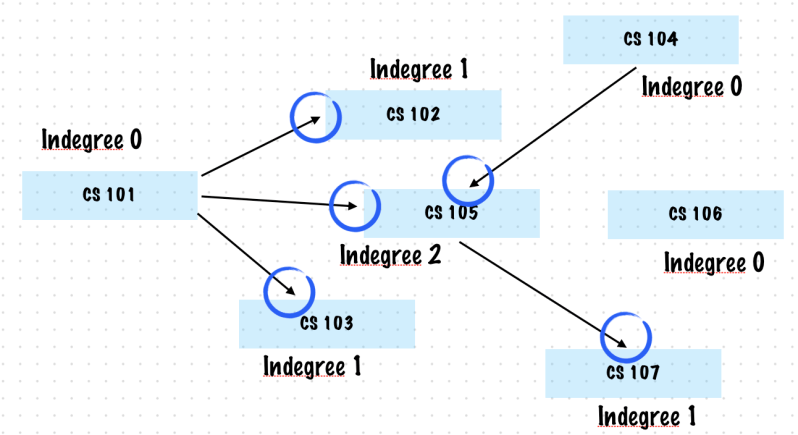
All nodes with indegree 0 are potential courses the student could start with
There are many schedules possible!
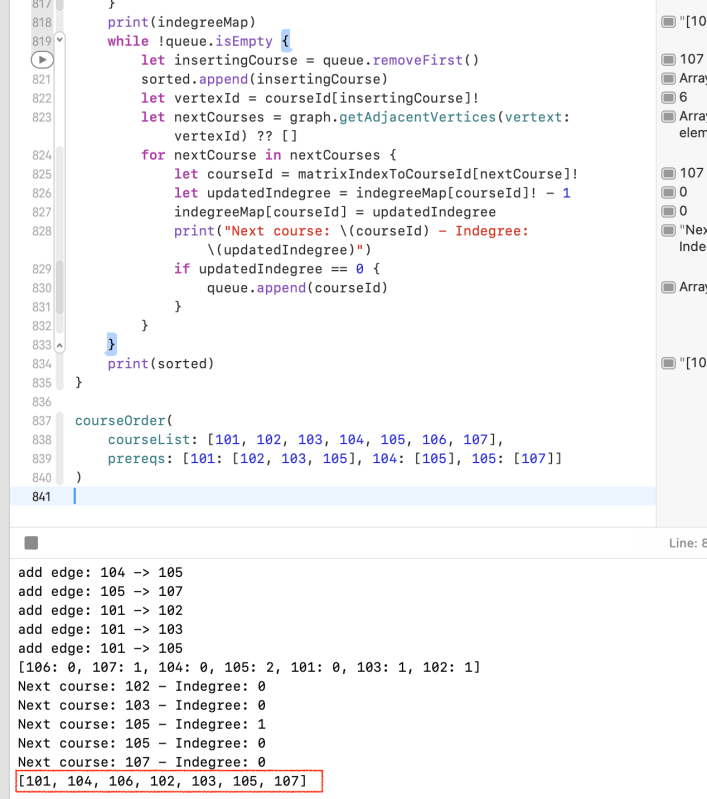
func courseOrder(courseList: [Int], prereqs: [Int: [Int]]) {
let graph = AdjacencyMatrix(vertices: courseList, graphType: .directed)
//You need this because Matrix used row and col start from 0 to number of vertices.
var courseId = [Int: Int]()
var matrixIndexToCourseId = [Int: Int]()
for (index, course) in courseList.enumerated() {
courseId[course] = index
matrixIndexToCourseId[index] = course
}
//Link Edges
for (preCourse, nextCourse) in prereqs {
for next in nextCourse {
print("add edge: \(preCourse) -> \(next)")
let preCourseId = courseId[preCourse]
let nextId = courseId[next]
graph.addEdge(src: preCourseId!, dst: nextId!)
}
}
var indegreeMap = [Int: Int]()
//Int is courseId not a Index
var queue = [Int]()
var sorted = [Int]()
for v in courseList {
//VertextId will be 0..<numberOfVertices
let vertexId = courseId[v]!
let indegree = graph.getIndegree(vertext: vertexId)
indegreeMap[v] = indegree
//Can take this course
if indegree == 0 {
queue.append(v)
}
}
print(indegreeMap)
while !queue.isEmpty {
let insertingCourse = queue.removeFirst()
sorted.append(insertingCourse)
let vertexId = courseId[insertingCourse]!
let nextCourses = graph.getAdjacentVertices(vertext: vertexId) ?? []
for nextCourse in nextCourses {
let courseId = matrixIndexToCourseId[nextCourse]!
let updatedIndegree = indegreeMap[courseId]! - 1
indegreeMap[courseId] = updatedIndegree
print("Next course: \(courseId) - Indegree: \(updatedIndegree)")
if updatedIndegree == 0 {
queue.append(courseId)
}
}
}
print(sorted)
}
courseOrder(
courseList: [101, 102, 103, 104, 105, 106, 107],
prereqs: [101: [102, 103, 105], 104: [105], 105: [107]]
)
Leave a Reply