✍️ Note

Some codes are sourced from Loony Corn’s Udemy Course (https://www.udemy.com/user/janani-ravi-2/). This post is for personal notes where I summarize the original contents to grasp the key concepts

Graph – Shortest Path Algorithms

Given a graph G with vertices V and edges E

Choose any vertex S – the source

What is the shortest path from S to a specific destination vertex D?

It is the path with the fewest hops to get from S to D

https://www.udemy.com/course/from-0-to-1-data-structures/learn/lecture/8506692#content

• There can be multiple paths to the same vertex with different distances
• Getting the shortest path is very similar to BFS
• We need to set up something called a Distance Table
• A Table of all vertices in a Graph

Type 1. Unweighted Graph, Find Shortest Path using Distance Table

Type 2. Weighted Graph, Dijkstra Algorithm: Find Shortest Path

Unlike unweighted graph, each edges having a weight or number. Its value can be negative or positive.

Dijkstra Algorithm is used for positive weights.

Bellman-Ford is used for negative weights too.

The algorithm here is quite similar to what we have discussed before in finding the shortest path in an Unweighted Graph (see Type 1 example)

There are 3 major differences

• We still use the Distance Table to store information
  • The distance from a Node now has to account for the weight of the edges traversed
  • distance[neighbors] = distance[vertex] + weight_of_edge[vertex, neighbor]
• Each vertex has neighbors
  • In a weighted graph – visit the neighbour which is connected by an edge with the Lowest Weight
  • Use a priority queue to implement this
    • To get the next vertex in the path, pop the element with the Lowest Weight -> It is called Greedy Algorithm
    • What is a Greedy Algorithm?
      • Greedy algorithms often fail to find the best solution
      • A greedy algorithm builds up a solution step by step
      • A every step it only optimizes for that particular step – It does not look at the overall problem
      • They do not operate on all the data so they may not see the Big Picture
      • Greedy algorithms are used for optimization problems
      • Greedy solutions are especially useful to find approximate solutions to very hard problems which are close to impossible to solve (Technical term NP Hard) E.g, The Traveling Salesman Problem
  • It’s possible to visit a vertex more than once
    • We check whether new distance (via the alternative route) is smaller than old distance
    • new distance = distance[vertex] + weight of edge[vertex, neighbour]
      • If new distance < original distance [neighbour] then Update the distance table. Put the vertex in Queue (Once Again)
      • Relaxation

Finding the shortest path in a weighted graph is called Dijkstra’s Algorithm

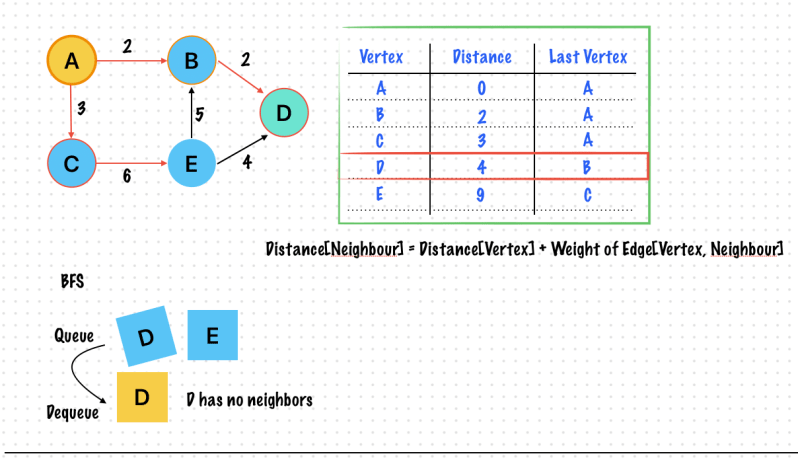
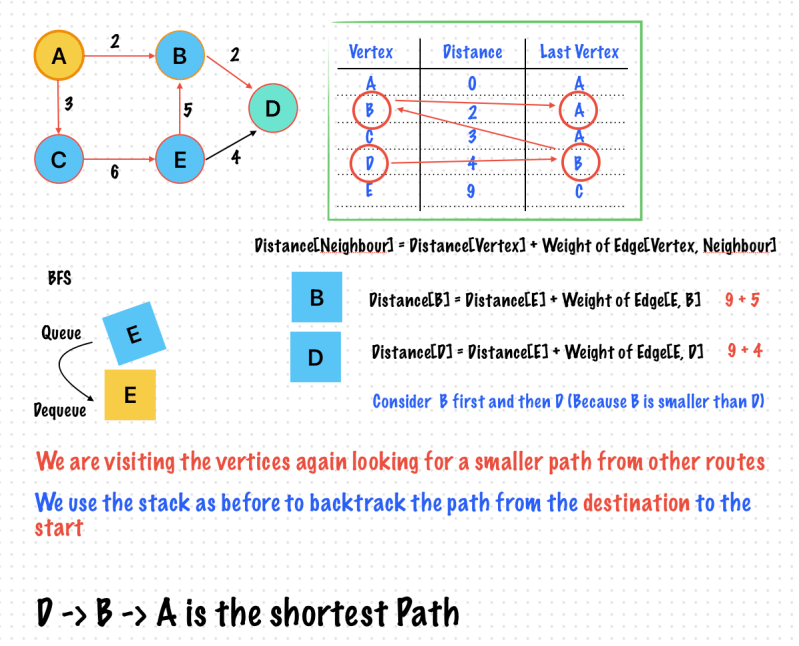
Shortest Path in Weighted Graph

The algorithm’s efficiency depends on how priority queue is implemented. It’s two operations – Updating the queue and Popping out from the queue determines the running time

Running Time is : O(ELogV) <- If Binary Heaps are used for priority queue

Running time is : O(E + V*V) <- If array is used for priority queue